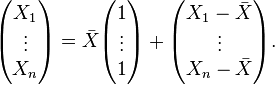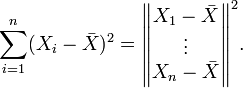Degrees of Freedom (statistics) - Degrees of Freedom of A Random Vector

Degrees of Freedom of A Random Vector

Geometrically, the degrees of freedom can be interpreted as the dimension of certain vector subspaces. As a starting point, suppose that we have a sample of n independent normally distributed observations,

This can be represented as an n-dimensional random vector:

Since this random vector can lie anywhere in n-dimensional space, it has n degrees of freedom.

Now, let be the sample mean. The random vector can be decomposed as the sum of the sample mean plus a vector of residuals:

$\begin{pmatrix} X_1\\ \vdots \\ X_n \end{pmatrix} = \bar X \begin{pmatrix} 1 \\ \vdots \\ 1 \end{pmatrix} + \begin{pmatrix} X_1-\bar{X} \\ \vdots \\ X_n-\bar{X} \end{pmatrix}.$

The first vector on the right-hand side is constrained to be a multiple of the vector of 1's, and the only free quantity is . It therefore has 1 degree of freedom.

The second vector is constrained by the relation . The first n − 1 components of this vector can be anything. However, once you know the first n − 1 components, the constraint tells you the value of the nth component. Therefore, this vector has n − 1 degrees of freedom.

Mathematically, the first vector is the orthogonal, or least-squares, projection of the data vector onto the subspace spanned by the vector of 1's. The 1 degree of freedom is the dimension of this subspace. The second residual vector is the least-squares projection onto the (n − 1)-dimensional orthogonal complement of this subspace, and has n − 1 degrees of freedom.

In statistical testing applications, often one isn't directly interested in the component vectors, but rather in their squared lengths. In the example above, the residual sum-of-squares is

$\sum_{i=1}^n (X_i - \bar{X})^2 = \begin{Vmatrix} X_1-\bar{X} \\ \vdots \\ X_n-\bar{X} \end{Vmatrix}^2.$

If the data points are normally distributed with mean 0 and variance, then the residual sum of squares has a scaled chi-squared distribution (scaled by the factor ), with n − 1 degrees of freedom. The degrees-of-freedom, here a parameter of the distribution, can still be interpreted as the dimension of an underlying vector subspace.

Likewise, the one-sample t-test statistic,

$\frac{ \sqrt{n} (\bar{X}-\mu_0) }{ \sqrt{\sum\limits_{i=1}^n (X_i-\bar{X})^2 / (n-1)} }$

follows a Student's t distribution with n − 1 degrees of freedom when the hypothesized mean is correct. Again, the degrees-of-freedom arises from the residual vector in the denominator.

Read more about this topic: Degrees Of Freedom (statistics)

Famous quotes containing the words degrees of, degrees, freedom and/or random:

“When a thought of Plato becomes a thought to me,—when a truth that fired the soul of Pindar fires mine, time is no more. When I feel that we two meet in a perception, that our two souls are tinged with the same hue, and do as it were run into one, why should I measure degrees of latitude, why should I count Egyptian years?”
—Ralph Waldo Emerson (1803–1882)

“How have I been able to live so long outside Nature without identifying myself with it? Everything lives, moves, everything corresponds; the magnetic rays, emanating either from myself or from others, cross the limitless chain of created things unimpeded; it is a transparent network that covers the world, and its slender threads communicate themselves by degrees to the planets and stars. Captive now upon earth, I commune with the chorus of the stars who share in my joys and sorrows.”
—Gérard De Nerval (1808–1855)

“Tyranny destroys or strengthens the individual; freedom enervates him, until he becomes no more than a puppet. Man has more chances of saving himself by hell than by paradise.”
—E.M. Cioran (b. 1911)

“Assemble, first, all casual bits and scraps
That may shake down into a world perhaps;
People this world, by chance created so,
With random persons whom you do not know—”
—Robert Graves (1895–1985)