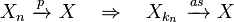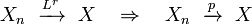Convergence of Random Variables - Properties

Properties

The chain of implications between the various notions of convergence are noted in their respective sections. They are, using the arrow notation:

\begin{matrix} \xrightarrow{L^s} & \underset{s>r\geq1}{\Rightarrow} & \xrightarrow{L^r} & & \\ & & \Downarrow & & \\ \xrightarrow{a.s.} & \Rightarrow & \xrightarrow{\ p\ } & \Rightarrow & \xrightarrow{\ d\ } \end{matrix}

These properties, together with a number of other special cases, are summarized in the following list:

  • Almost sure convergence implies convergence in probability:
    X_n\ \xrightarrow{as}\ X \quad\Rightarrow\quad X_n\ \xrightarrow{p}\ X
  • Convergence in probability implies there exists a sub-sequence which almost surely converges:
    X_n\ \xrightarrow{p}\ X \quad\Rightarrow\quad X_{k_n}\ \xrightarrow{as}\ X
  • Convergence in probability implies convergence in distribution:
    X_n\ \xrightarrow{p}\ X \quad\Rightarrow\quad X_n\ \xrightarrow{d}\ X
  • Convergence in r-th order mean implies convergence in probability:
    X_n\ \xrightarrow{L^r}\ X \quad\Rightarrow\quad X_n\ \xrightarrow{p}\ X
  • Convergence in r-th order mean implies convergence in lower order mean, assuming that both orders are greater than one:
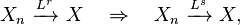    X_n\ \xrightarrow{L^r}\ X \quad\Rightarrow\quad X_n\ \xrightarrow{L^s}\ X, provided r ≥ s ≥ 1.
  • If Xn converges in distribution to a constant c, then Xn converges in probability to c:
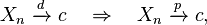    X_n\ \xrightarrow{d}\ c \quad\Rightarrow\quad X_n\ \xrightarrow{p}\ c, provided c is a constant.
  • If Xn converges in distribution to X and the difference between Xn and Yn converges in probability to zero, then Yn also converges in distribution to X:
    X_n\ \xrightarrow{d}\ X,\ \ |X_n-Y_n|\ \xrightarrow{p}\ 0\ \quad\Rightarrow\quad Y_n\ \xrightarrow{d}\ X
  • If Xn converges in distribution to X and Yn converges in distribution to a constant c, then the joint vector (Xn, Yn) converges in distribution to (X, c):
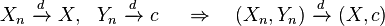    X_n\ \xrightarrow{d}\ X,\ \ Y_n\ \xrightarrow{d}\ c\ \quad\Rightarrow\quad (X_n,Y_n)\ \xrightarrow{d}\ (X,c) provided c is a constant.
    Note that the condition that Yn converges to a constant is important, if it were to converge to a random variable Y then we wouldn’t be able to conclude that (Xn, Yn) converges to (X, Y).
  • If Xn converges in probability to X and Yn converges in probability to Y, then the joint vector (Xn, Yn) converges in probability to (X, Y):
    X_n\ \xrightarrow{p}\ X,\ \ Y_n\ \xrightarrow{p}\ Y\ \quad\Rightarrow\quad (X_n,Y_n)\ \xrightarrow{p}\ (X,Y)
  • If Xn converges in probability to X, and if P(|Xn| ≤ b) = 1 for all n and some b, then Xn converges in rth mean to X for all r ≥ 1. In other words, if Xn converges in probability to X and all random variables Xn are almost surely bounded above and below, then Xn converges to X also in any rth mean.
  • Almost sure representation. Usually, convergence in distribution does not imply convergence almost surely. However for a given sequence {Xn} which converges in distribution to X0 it is always possible to find a new probability space (Ω, F, P) and random variables {Yn, n = 0,1,…} defined on it such that Yn is equal in distribution to Xn for each n ≥ 0, and Yn converges to Y0 almost surely.
  • If for all ε > 0,
then we say that Xn converges almost completely, or almost in probability towards X. When Xn converges almost completely towards X then it also converges almost surely to X. In other words, if Xn converges in probability to X sufficiently quickly (i.e. the above sequence of tail probabilities is summable for all ε > 0), then Xn also converges almost surely to X. This is a direct implication from the Borel-Cantelli lemma.
  • If Sn is a sum of n real independent random variables:
then Sn converges almost surely if and only if Sn converges in probability.
  • The dominated convergence theorem gives sufficient conditions for almost sure convergence to imply L1-convergence:
\left. \begin{array}{ccc} X_n\xrightarrow{a.s.} X \\ \\ |X_n| < Y \\ \\ \mathrm{E}(Y) < \infty \end{array}\right\} \quad\Rightarrow \quad X_n\xrightarrow{L^1} X
  • A necessary and sufficient condition for L1 convergence is and the sequence (Xn) is uniformly integrable.

Read more about this topic:  Convergence Of Random Variables

Famous quotes containing the word properties:

    “The reason why men enter into society, is the preservation of their property; and the end why they choose and authorize a legislative, is, that there may be laws made, and rules set, as guards and fences to the properties of all the members of the society: to limit the power, and moderate the dominion, of every part and member of the society.”
    —John Locke (1632–1704)

    “A drop of water has the properties of the sea, but cannot exhibit a storm. There is beauty of a concert, as well as of a flute; strength of a host, as well as of a hero.”
    —Ralph Waldo Emerson (1803–1882)