Calibration Curve - Error in Calibration Curve Results

Error in Calibration Curve Results

As expected, the concentration of the unknown will have some error which can be calculated from the formula below. This formula assumes that a linear relationship is observed for all the standards. It is important to note that the error in the concentration will be minimal if the signal from the unknown lies in the middle of the signals of all the standards (the term goes to zero if )

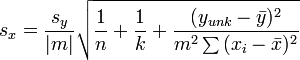
s_x=\frac{s_y}{|m|}\sqrt{\frac{1}{n}+\frac{1}{k}+\frac{(y_{unk}-\bar{y})^2}{m^2\sum{(x_i-\bar{x})^2}}}

  • is the standard deviation in the residuals
  • is the slope of the line
  • is the y-intercept of the line
  • is the number standards
  • is the number of replicate unknowns
  • is the measurement of the unknown
  • is the average measurement of the standards
  • are the concentrations of the standards
  • is the average concentration of the standards

Read more about this topic:  Calibration Curve

Famous quotes containing the words error, curve and/or results:

    “What has been the effect of [religious] coercion? To make one half the world fools, and the other half hypocrites. To support roguery and error all over the earth.”
    —Thomas Jefferson (1743–1826)

    “In philosophical inquiry, the human spirit, imitating the movement of the stars, must follow a curve which brings it back to its point of departure. To conclude is to close a circle.”
    —Charles Baudelaire (1821–1867)

    “It would be easy ... to regard the whole of world 3 as timeless, as Plato suggested of his world of Forms or Ideas.... I propose a different view—one which, I have found, is surprisingly fruitful. I regard world 3 as being essentially the product of the human mind.... More precisely, I regard the world 3 of problems, theories, and critical arguments as one of the results of the evolution of human language, and as acting back on this evolution.”
    —Karl Popper (1902–1994)