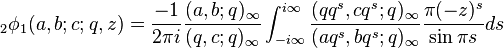Basic Hypergeometric Series - Watson's Contour Integral

Watson's Contour Integral

As an analogue of the Barnes integral for the hypergeometric series, Watson showed that

{}_2\phi_1(a,b;c;q,z) = \frac{-1}{2\pi i}\frac{(a,b;q)_\infty}{(q,c;q)_\infty} \int_{-i\infty}^{i\infty}\frac{(qq^s,cq^s;q)_\infty}{(aq^s,bq^s;q)_\infty}\frac{\pi(-z)^s}{\sin \pi s}ds

where the poles of lie to the left of the contour and the remaining poles lie to the right. There is a similar contour integral for r+1φr. This contour integral gives an analytic continuation of the basic hypergeometric function in z.

Read more about this topic:  Basic Hypergeometric Series

Famous quotes containing the words watson, contour and/or integral:

    “Now there are nine. There’ll be more, many more. They’re coming for me now. And then they’ll come for you.”
    —Robb White, and William Castle. Watson Pritchard (Elisha Cook)

    “The living language is like a cowpath: it is the creation of the cows themselves, who, having created it, follow it or depart from it according to their whims or their needs. From daily use, the path undergoes change. A cow is under no obligation to stay in the narrow path she helped make, following the contour of the land, but she often profits by staying with it and she would be handicapped if she didn’t know where it was or where it led to.”
    —E.B. (Elwyn Brooks)

    “Self-centeredness is a natural outgrowth of one of the toddler’s major concerns: What is me and what is mine...? This is why most toddlers are incapable of sharing ... to a toddler, what’s his is what he can get his hands on.... When something is taken away from him, he feels as though a piece of him—an integral piece—is being torn from him.”
    —Lawrence Balter (20th century)