Angular Diameter Distance

The angular diameter distance is a distance measure used in astronomy. The angular diameter distance to an object is defined in terms of the object's actual size, and the angular size of the object as viewed from earth.
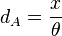
d_A= \frac{x}{\theta}
The angular diameter distance depends on the assumed cosmology of the universe. The angular diameter distance to an object at redshift, is expressed in terms of the comoving distance, as:
d_A = \frac{r(\chi)}{1+z}
Where is defined as:
r(\chi) = \begin{cases} \sin \left( \sqrt{-\Omega_k} H_0 \chi \right)/\left(H_0\sqrt{|\Omega_k|}\right) & \Omega_k < 0\\ \chi & \Omega_k=0 \\ \sinh \left( \sqrt{\Omega_k} H_0 \chi \right)/\left(H_0\sqrt{|\Omega_k|}\right) & \Omega_k >0 \end{cases}
Where is the curvature density and is the value of the Hubble parameter today.

In the currently favoured geometric model of our Universe, the "angular diameter distance" of an object is a good approximation to the "real distance", i.e. the proper distance when the light left the object. Note that beyond a certain redshift, the angular diameter distance gets smaller with increasing redshift. In other words an object "behind" another of the same size, beyond a certain redshift (roughly z=1.5), appears larger on the sky, and would therefore have a smaller "angular diameter distance".

Read more about Angular Diameter Distance:  Angular Size Redshift Relation

Famous quotes containing the word distance:

    “It is painful to recall a past intensity, to estimate your distance from the Belsen heap, to make your peace with numbers. Just to get up each morning is to make a kind of peace.”
    —Leonard Cohen (b. 1934)