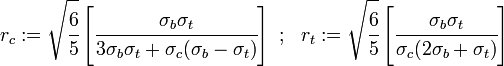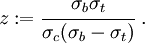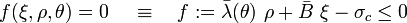Willam-Warnke Yield Criterion - Willam-Warnke Yield Function

Willam-Warnke Yield Function

In the original paper, the three-parameter Willam-Warnke yield function was expressed as

$f := \cfrac{1}{3z}~\cfrac{I_1}{\sigma_c} + \sqrt{\cfrac{2}{5}}~\cfrac{1}{r(\theta)}\cfrac{\sqrt{J_2}}{\sigma_c} - 1 \le 0$

where is the first invariant of the stress tensor, is the second invariant of the deviatoric part of the stress tensor, is the yield stress in uniaxial compression, and is the Lode angle given by

$\theta = \tfrac{1}{3}\cos^{-1}\left(\cfrac{3\sqrt{3}}{2}~\cfrac{J_3}{J_2^{3/2}}\right) ~.$

The locus of the boundary of the stress surface in the deviatoric stress plane is expressed in polar coordinates by the quantity which is given by

$r(\theta) := \cfrac{u(\theta)+v(\theta)}{w(\theta)}$

where

$\begin{align} u(\theta) := & 2~r_c~(r_c^2-r_t^2)~\cos\theta \\ v(\theta) := & r_c~(2~r_t - r_c)\sqrt{4~(r_c^2 - r_t^2)~\cos^2\theta + 5~r_t^2 - 4~r_t~r_c} \\ w(\theta) := & 4(r_c^2 - r_t^2)\cos^2\theta + (r_c-2~r_t)^2 \end{align}$

The quantities and describe the position vectors at the locations and can be expressed in terms of as

$r_c := \sqrt{\cfrac{6}{5}}\left ~;~~ r_t := \sqrt{\cfrac{6}{5}}\left$

The parameter in the model is given by

$z := \cfrac{\sigma_b\sigma_t}{\sigma_c(\sigma_b-\sigma_t)} ~.$

The Haigh-Westergaard representation of the Willam-Warnke yield condition can be written as

$f(\xi, \rho, \theta) = 0 \, \quad \equiv \quad f := \bar{\lambda}(\theta)~\rho + \bar{B}~\xi - \sigma_c \le 0$

where

$\bar{B} := \cfrac{1}{\sqrt{3}~z} ~;~~ \bar{\lambda} := \cfrac{1}{\sqrt{5}~r(\theta)} ~.$

Read more about this topic: Willam-Warnke Yield Criterion

Famous quotes containing the words yield and/or function:

“Time is here and you’ll go his way.
Your lung is waiting in the death market.
Your face beside me will grow indifferent.
Darling, you will yield up your belly and be
cored like an apple.”
—Anne Sexton (1928–1974)

“Advocating the mere tolerance of difference between women is the grossest reformism. It is a total denial of the creative function of difference in our lives. Difference must be not merely tolerated, but seen as a fund of necessary polarities between which our creativity can spark like a dialectic.”
—Audre Lorde (1934–1992)