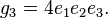Weierstrass's Elliptic Functions - The Constants e1, e2 and e3 | Constants e1, e2<> e3<>

The Constants e₁, e₂ and e₃

Consider the cubic polynomial equation 4t3 − g₂t − g₃ = 0 with roots e₁, e₂, and e₃. If the discriminant Δ = g₂3 − 27g₃2 is not zero, no two of these roots are equal. Since the quadratic term of this cubic polynomial is zero, the roots are related by the equation

$e_1+e_2+e_3=0. \,$

The linear and constant coefficients (g₂ and g₃, respectively) are related to the roots by the equations

$g_2 = -4 \left( e_1 e_2 + e_1 e_3 + e_2 e_3 \right) = 2 \left( e_1^2 + e_2^2 + e_3^2 \right) \,$

$g_3 = 4 e_1 e_2 e_3. \,$

In the case of real invariants, the sign of determines the nature of the roots. If, all three are real and it is conventional to name them so that . If, it is conventional to write (where, ), whence and is real and non-negative.

The half-periods ω₁/2 and ω₂/2 of Weierstrass' elliptic function are related to the roots

$\wp(\omega_1/2)=e_1\qquad \wp(\omega_2/2)=e_2\qquad \wp(\omega_3/2)=e_3$

where . Since the square of the derivative of Weierstrass's elliptic function equals the above cubic polynomial of the function's value, for . Conversely, if the function's value equals a root of the polynomial, the derivative is zero.

If g₂ and g₃ are real and Δ > 0, the e_i are all real, and is real on the perimeter of the rectangle with corners 0, ω₃, ω₁ + ω₃, and ω₁. If the roots are ordered as above (e₁ > e₂ > e₃), then the first half-period is completely real

$\omega_{1}/2 = \int_{e_{1}}^{\infty} \frac{dz}{\sqrt{4z^{3} - g_{2}z - g_{3}}}$

whereas the third half-period is completely imaginary

$\omega_{3}/2 = i \int_{-e_{3}}^{\infty} \frac{dz}{\sqrt{4z^{3} - g_{2}z - g_{3}}}.$

Read more about this topic: Weierstrass's Elliptic Functions