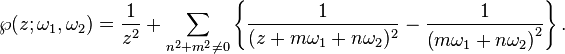Weierstrass's Elliptic Functions - Definitions

Definitions

The Weierstrass elliptic function can be defined in three closely related ways, each of which possesses certain advantages. One is as a function of a complex variable z and a lattice Λ in the complex plane. Another is in terms of z and two complex numbers ω1 and ω2 defining a pair of generators, or periods, for the lattice. The third is in terms z and of a modulus τ in the upper half-plane. This is related to the previous definition by τ = ω2/ω1, which by the conventional choice on the pair of periods is in the upper half-plane. Using this approach, for fixed z the Weierstrass functions become modular functions of τ.

In terms of the two periods, Weierstrass's elliptic function is an elliptic function with periods ω1 and ω2 defined as

\wp(z;\omega_1,\omega_2)=\frac{1}{z^2}+ \sum_{n^2+m^2 \ne 0} \left\{ \frac{1}{(z+m\omega_1+n\omega_2)^2}- \frac{1}{\left(m\omega_1+n\omega_2\right)^2} \right\}.

Then are the points of the period lattice, so that

for any pair of generators of the lattice defines the Weierstrass function as a function of a complex variable and a lattice.

If is a complex number in the upper half-plane, then

\wp(z;\tau) = \wp(z;1,\tau) = \frac{1}{z^2} + \sum_{n^2+m^2 \ne 0}\left\{ {1 \over (z+m+n\tau)^2} - {1 \over (m+n\tau)^2}\right\}.

The above sum is homogeneous of degree minus two, from which we may define the Weierstrass ℘ function for any pair of periods, as

We may compute ℘ very rapidly in terms of theta functions; because these converge so quickly, this is a more expeditious way of computing ℘ than the series we used to define it. The formula here is

There is a second-order pole at each point of the period lattice (including the origin). With these definitions, is an even function and its derivative with respect to z, ℘′, an odd function.

Further development of the theory of elliptic functions shows that the condition on Weierstrass's function is determined up to addition of a constant and multiplication by a non-zero constant by the condition on the poles alone, amongst all meromorphic functions with the given period lattice.

Read more about this topic:  Weierstrass's Elliptic Functions

Famous quotes containing the word definitions:

    “Lord Byron is an exceedingly interesting person, and as such is it not to be regretted that he is a slave to the vilest and most vulgar prejudices, and as mad as the winds?
    There have been many definitions of beauty in art. What is it? Beauty is what the untrained eyes consider abominable.”
    —Edmond De Goncourt (1822–1896)

    “What I do not like about our definitions of genius is that there is in them nothing of the day of judgment, nothing of resounding through eternity and nothing of the footsteps of the Almighty.”
    —G.C. (Georg Christoph)

    “The loosening, for some people, of rigid role definitions for men and women has shown that dads can be great at calming babies—if they take the time and make the effort to learn how. It’s that time and effort that not only teaches the dad how to calm the babies, but also turns him into a parent, just as the time and effort the mother puts into the babies turns her into a parent.”
    —Pamela Patrick Novotny (20th century)