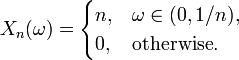Uniform Integrability - Related Corollaries

Related Corollaries

The following results apply.

Definition 1 could be rewritten by taking the limits as

A non-UI sequence. Let, and define

$X_n(\omega) = \begin{cases} n, & \omega\in (0,1/n), \\ 0, & \text{otherwise.} \end{cases}$

Clearly, and indeed for all n. However,

and comparing with definition 1, it is seen that the sequence is not uniformly integrable.

By using Definition 2 in the above example, it can be seen that the first clause is not satisfied as the s are not bounded in . If is a UI random variable, by splitting

and bounding each of the two, it can be seen that a uniformly integrable random variable is always bounded in . It can also be shown that any random variable will satisfy clause 2 in Definition 2.

If any sequence of random variables is dominated by an integrable, non-negative : that is, for all ω and n,

then the class of random variables is uniformly integrable.

A class of random variables bounded in is uniformly integrable.

Read more about this topic: Uniform Integrability

Famous quotes containing the word related:

“Becoming responsible adults is no longer a matter of whether children hang up their pajamas or put dirty towels in the hamper, but whether they care about themselves and others—and whether they see everyday chores as related to how we treat this planet.”
—Eda Le Shan (20th century)