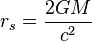Two-body Problem in General Relativity - Schwarzschild Solution

Schwarzschild Solution

An exact solution to the Einstein field equations is the Schwarzschild metric, which corresponds to the external gravitational field of a stationary, uncharged, non-rotating, spherically symmetric body of mass M. It is characterized by a length scale r_s, known as the Schwarzschild radius, which is defined by the formula

where G is the gravitational constant. The classical Newtonian theory of gravity is recovered in the limit as the ratio r_s/r goes to zero. In that limit, the metric returns to that defined by special relativity.

In practice, this ratio is almost always extremely small. For example, the Schwarzschild radius r_s of the Earth is roughly 9 mm (3⁄₈ inch); at the surface of the Earth, the corrections to Newtonian gravity are only one part in a billion. The Schwarzschild radius of the Sun is much larger, roughly 2953 meters, but at its surface, the ratio r_s/r is roughly 4 parts in a million. A white dwarf star is much denser, but even here the ratio at its surface is roughly 250 parts in a million. The ratio only becomes large close to ultra-dense objects such as neutron stars (where the ratio is roughly 50%) and black holes.