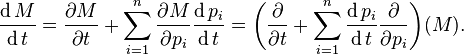Total Derivative - Differentiation With Indirect Dependencies

Differentiation With Indirect Dependencies

Suppose that f is a function of two variables, x and y. Normally these variables are assumed to be independent. However, in some situations they may be dependent on each other. For example y could be a function of x, constraining the domain of f to a curve in R2. In this case the partial derivative of f with respect to x does not give the true rate of change of f with respect to changing x because changing x necessarily changes y. The total derivative takes such dependencies into account.

For example, suppose

The rate of change of f with respect to x is usually the partial derivative of f with respect to x; in this case,

However, if y depends on x, the partial derivative does not give the true rate of change of f as x changes because it holds y fixed.

Suppose we are constrained to the line

then

In that case, the total derivative of f with respect to x is

Instead of immediately substituting for y in terms of x, this can be found equivalently using the chain rule:

Notice that this is not equal to the partial derivative:

While one can often perform substitutions to eliminate indirect dependencies, the chain rule provides for a more efficient and general technique. Suppose M(t, p₁, ..., p_n) is a function of time t and n variables which themselves depend on time. Then, the total time derivative of M is

The chain rule for differentiating a function of several variables implies that

${\operatorname{d}M \over \operatorname{d}t} = \frac{\partial M}{\partial t} + \sum_{i=1}^n \frac{\partial M}{\partial p_i}\frac{\operatorname{d}p_i}{\operatorname{d}t} = \biggl(\frac{\partial}{\partial t} + \sum_{i=1}^n \frac{\operatorname{d}p_i}{\operatorname{d}t}\frac{\partial}{\partial p_i}\biggr)(M).$

This expression is often used in physics for a gauge transformation of the Lagrangian, as two Lagrangians that differ only by the total time derivative of a function of time and the n generalized coordinates lead to the same equations of motion. An interesting example concerns the resolution of causality concerning the Wheeler-Feynman time-symmetric theory. The operator in brackets (in the final expression) is also called the total derivative operator (with respect to t).

For example, the total derivative of f(x(t), y(t)) is

Here there is no ∂f / ∂t term since f itself does not depend on the independent variable t directly.

Read more about this topic: Total Derivative

Famous quotes containing the word indirect:

“Imagination is always the fabric of social life and the dynamic of history. The influence of real needs and compulsions, of real interests and materials, is indirect because the crowd is never conscious of it.”
—Simone Weil (1909–1943)