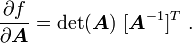Derivative of The Determinant of A Second-order Tensor
The derivative of the determinant of a second order tensor is given by
In an orthonormal basis, the components of can be written as a matrix A. In that case, the right hand side corresponds the cofactors of the matrix.
-
Proof Let be a second order tensor and let . Then, from the definition of the derivative of a scalar valued function of a tensor, we have
Recall that we can expand the determinant of a tensor in the form of a characteristic equation in terms of the invariants using (note the sign of λ)
Using this expansion we can write
Recall that the invariant is given by
Hence,
Invoking the arbitrariness of we then have
Read more about this topic: Tensor Derivative (continuum Mechanics)
Famous quotes containing the word derivative:
“Poor John Field!—I trust he does not read this, unless he will improve by it,—thinking to live by some derivative old-country mode in this primitive new country.... With his horizon all his own, yet he a poor man, born to be poor, with his inherited Irish poverty or poor life, his Adam’s grandmother and boggy ways, not to rise in this world, he nor his posterity, till their wading webbed bog-trotting feet get talaria to their heels.”
—Henry David Thoreau (1817–1862)


![\begin{align} \frac{\partial f}{\partial \boldsymbol{A}}:\boldsymbol{T} & = \left.\cfrac{d}{d\alpha} \left[\alpha^3~\det(\boldsymbol{A})~ \left(\cfrac{1}{\alpha^3} + I_1(\boldsymbol{A}^{-1}\cdot\boldsymbol{T})~\cfrac{1}{\alpha^2} + I_2(\boldsymbol{A}^{-1}\cdot\boldsymbol{T})~\cfrac{1}{\alpha} + I_3(\boldsymbol{A}^{-1}\cdot\boldsymbol{T})\right) \right] \right|_{\alpha=0} \\ & = \left.\det(\boldsymbol{A})~\cfrac{d}{d\alpha} \left[ 1 + I_1(\boldsymbol{A}^{-1}\cdot\boldsymbol{T})~\alpha + I_2(\boldsymbol{A}^{-1}\cdot\boldsymbol{T})~\alpha^2 + I_3(\boldsymbol{A}^{-1}\cdot\boldsymbol{T})~\alpha^3 \right] \right|_{\alpha=0} \\ & = \left.\det(\boldsymbol{A})~\left[I_1(\boldsymbol{A}^{-1}\cdot\boldsymbol{T}) + 2~I_2(\boldsymbol{A}^{-1}\cdot\boldsymbol{T})~\alpha + 3~I_3(\boldsymbol{A}^{-1}\cdot\boldsymbol{T})~\alpha^2 \right] \right|_{\alpha=0} \\ & = \det(\boldsymbol{A})~I_1(\boldsymbol{A}^{-1}\cdot\boldsymbol{T}) ~. \end{align}](http://upload.wikimedia.org/math/7/f/3/7f31e3d92a4861d3e8592cf9b79f25c4.png)