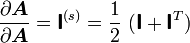Tensor Derivative (continuum Mechanics) - Derivative of A Second-order Tensor With Respect To Itself

Derivative of A Second-order Tensor With Respect To Itself

Let be a second order tensor. Then

$\frac{\partial \boldsymbol{A}}{\partial \boldsymbol{A}}:\boldsymbol{T} = \left_{\alpha = 0} = \boldsymbol{T} = \boldsymbol{\mathsf{I}}:\boldsymbol{T}$

Therefore,

$\frac{\partial \boldsymbol{A}}{\partial \boldsymbol{A}} = \boldsymbol{\mathsf{I}}$

Here is the fourth order identity tensor. In index notation with respect to an orthonormal basis

$\boldsymbol{\mathsf{I}} = \delta_{ik}~\delta_{jl}~\mathbf{e}_i\otimes\mathbf{e}_j\otimes\mathbf{e}_k\otimes\mathbf{e}_l$

This result implies that

$\frac{\partial \boldsymbol{A}^T}{\partial \boldsymbol{A}}:\boldsymbol{T} = \boldsymbol{\mathsf{I}}^T:\boldsymbol{T} = \boldsymbol{T}^T$

where

$\boldsymbol{\mathsf{I}}^T = \delta_{jk}~\delta_{il}~\mathbf{e}_i\otimes\mathbf{e}_j\otimes\mathbf{e}_k\otimes\mathbf{e}_l$

Therefore, if the tensor is symmetric, then the derivative is also symmetric and we get

$\frac{\partial \boldsymbol{A}}{\partial \boldsymbol{A}} = \boldsymbol{\mathsf{I}}^{(s)} = \frac{1}{2}~(\boldsymbol{\mathsf{I}} + \boldsymbol{\mathsf{I}}^T)$

where the symmetric fourth order identity tensor is

$\boldsymbol{\mathsf{I}}^{(s)} = \frac{1}{2}~(\delta_{ik}~\delta_{jl} + \delta_{il}~\delta_{jk}) ~\mathbf{e}_i\otimes\mathbf{e}_j\otimes\mathbf{e}_k\otimes\mathbf{e}_l$

Read more about this topic: Tensor Derivative (continuum Mechanics)

Famous quotes containing the words derivative and/or respect:

“When we say “science” we can either mean any manipulation of the inventive and organizing power of the human intellect: or we can mean such an extremely different thing as the religion of science the vulgarized derivative from this pure activity manipulated by a sort of priestcraft into a great religious and political weapon.”
—Wyndham Lewis (1882–1957)

“What cannot stand must fall; and the measure of our sincerity and therefore of the respect of men, is the amount of health and wealth we will hazard in the defence of our right. An old farmer, my neighbor across the fence, when I ask him if he is not going to town-meeting, says: “No, ‘t is no use balloting, for it will not stay; but what you do with the gun will stay so.””
—Ralph Waldo Emerson (1803–1882)