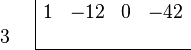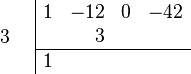Synthetic Division - Regular Synthetic Division

Regular Synthetic Division

The first example is synthetic division with only a monic linear denominator .

Write the coefficients of the polynomial to be divided at the top (the zero is for the unseen 0x).

$\begin{array}{cc} \begin{array}{r} \\ \\ \end{array} & \begin{array}{|rrrr} 1 & -12 & 0 & -42 \\ & & & \\ \hline \end{array} \end{array}$

Negate the coefficients of the divisor.

$\begin{array}{rr} -1x & + 3 \end{array}$

Write in every coefficient of the divisor but the first one on the left.

$\begin{array}{cc} \begin{array}{r} \\ 3 \\ \end{array} & \begin{array}{|rrrr} 1 & -12 & 0 & -42 \\ & & & \\ \hline \end{array} \end{array}$

Note the change of sign from −3 to 3. "Drop" the first coefficient after the bar to the last row.

$\begin{array}{cc} \begin{array}{r} \\ 3 \\ \\ \end{array} & \begin{array}{|rrrr} 1 & -12 & 0 & -42 \\ & & & \\ \hline 1 & & & \\ \end{array} \end{array}$

Multiply the dropped number by the number before the bar, and place it in the next column.

$\begin{array}{cc} \begin{array}{r} \\ 3 \\ \\ \end{array} & \begin{array}{|rrrr} 1 & -12 & 0 & -42 \\ & 3 & & \\ \hline 1 & & & \\ \end{array} \end{array}$

Perform an addition in the next column.

$\begin{array}{cc} \begin{array}{c} \\ 3 \\ \\ \end{array} & \begin{array}{|rrrr} 1 & -12 & 0 & -42 \\ & 3 & & \\ \hline 1 & -9 & & \\ \end{array} \end{array}$

Repeat the previous two steps and the following is obtained:

$\begin{array}{cc} \begin{array}{c} \\ 3 \\ \\ \end{array} & \begin{array}{|rrrr} 1 & -12 & 0 & -42 \\ & 3 & -27 & -81 \\ \hline 1 & -9 & -27 & -123 \end{array} \end{array}$

Count the terms to the left of the bar. Since there is only one, the remainder has degree zero. Mark the separation with a vertical bar.

$\begin{array}{rrr|r} 1 & -9 & -27 & -123 \end{array}$

The terms are written with increasing degree from right to left beginning with degree zero for both the remainder and the result.

$\begin{array}{rrr|r} 1x^2 & -9x & -27 & -123 \end{array}$

The result of our division is:

Evaluating Polynomials by the Remainder Theorem

The above form of synthetic division is useful in the context of the Polynomial remainder theorem for evaluating univariate polynomials. To summarize, the value of at is equal to the remainder of . The advantage of calculating the value this way is that it requires just over half as many multiplication steps as naive evaluation. An alternative evaluation strategy is Horner's method.

Read more about this topic: Synthetic Division

Famous quotes containing the words regular, synthetic and/or division:

“It was inspiriting to hear the regular dip of the paddles, as if they were our fins or flippers, and to realize that we were at length fairly embarked. We who had felt strangely as stage-passengers and tavern-lodgers were suddenly naturalized there and presented with the freedom of the lakes and woods.”
—Henry David Thoreau (1817–1862)

“In every philosophical school, three thinkers succeed one another in the following way: the first produces out of himself the sap and seed, the second draws it out into threads and spins a synthetic web, and the third waits in this web for the sacrificial victims that are caught in it—and tries to live off philosophy.”
—Friedrich Nietzsche (1844–1900)

“For in the division of the nations of the whole earth he set a ruler over every people; but Israel is the Lord’s portion: whom, being his firstborn, he nourisheth with discipline, and giving him the light of his love doth not forsake him. Therefore all their works are as the sun before him, and his eyes are continually upon their ways.”
—Apocrypha. Ecclesiasticus 17:17-9.