Symmetry (physics) - Mathematics

Mathematics

Continuous symmetries in physics preserve transformations. One can specify a symmetry by showing how a very small transformation affects various particle fields. The commutator of two of these infinitessimal transformations are equivalent to a third infinitessimal transformation of the same kind hence they form a Lie algebra.

A general coordinate transformation (also known as a diffeomorphism) has the infinitessimal effect on a scalar, spinor and vector field for example:

$\delta\phi(x) = h^{\mu}(x)\partial_{\mu}\phi(x)$

$\delta\psi^\alpha(x) = h^{\mu}(x)\partial_{\mu}\psi^\alpha(x) + \partial_\mu h_\nu(x) \sigma_{\mu\nu}^{\alpha \beta} \psi^{\beta}(x)$

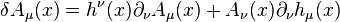
$\delta A_\mu(x) = h^{\nu}(x)\partial_{\nu}A_\mu(x) + A_\nu(x)\partial_\nu h_\mu(x)$

for a general field, . Without gravity only the Poincaré symmetries are preserved which restricts to be of the form:

$h^{\mu}(x) = M^{\mu \nu}x_\nu + P^\mu$

where M is an antisymmetric matrix (giving the Lorentz and rotational symmetries) and P is a general vector (giving the translational symmetries). Other symmetries affect multiple fields simultaneously. For example local gauge transformations apply to both a vector and spinor field:

$\delta\psi^\alpha(x) = \lambda(x).\tau^{\alpha\beta}\psi^\beta(x)$

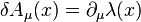
$\delta A_\mu(x) = \partial_\mu \lambda(x)$

where are generators of a particular Lie group. So far the transformations on the right have only included fields of the same type. Supersymmetries are defined according to how the mix fields of different types.

Another symmetry which is part of some theories of physics and not in others is scale invariance which involve Weyl transformations of the following kind:

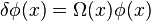
$\delta \phi(x) = \Omega(x) \phi(x)$

If the fields have this symmetry then it can be shown that the field theory is almost certainly conformally invariant also. This means that in the absence of gravity h(x) would restricted to the form:

$h^{\mu}(x) = M^{\mu \nu}x_\nu + P^\mu + D x_\mu + K^{\mu} |x|^2 - 2 K^\nu x_\nu x_\mu$

with D generating scale transformations and K generating special conformal transformations. For example N=4 super-Yang-Mills theory has this symmetry while General Relativity doesn't although other theories of gravity such as conformal gravity do. The 'action' of a field theory is an invariant under all the symmetries of the theory. Much of modern theoretical physics is to do with speculating on the various symmetries the Universe may have and finding the invariants to construct field theories as models.

In string theories, since a string can be decomposed into an infinite number of particle fields, the symmetries on the string world sheet is equivalent to special transformations which mix an infinite number of fields.

Read more about this topic: Symmetry (physics)

Famous quotes containing the word mathematics:

“... though mathematics may teach a man how to build a bridge, it is what the Scotch Universities call the humanities, that teach him to be civil and sweet-tempered.”
—Amelia E. Barr (1831–1919)

“Mathematics alone make us feel the limits of our intelligence. For we can always suppose in the case of an experiment that it is inexplicable because we don’t happen to have all the data. In mathematics we have all the data ... and yet we don’t understand. We always come back to the contemplation of our human wretchedness. What force is in relation to our will, the impenetrable opacity of mathematics is in relation to our intelligence.”
—Simone Weil (1909–1943)