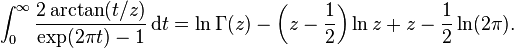Stirling's Approximation - A Convergent Version of Stirling's Formula

A Convergent Version of Stirling's Formula

Thomas Bayes showed, in a letter to John Canton published by the Royal Society in 1763, that Stirling's formula did not give a convergent series.

Obtaining a convergent version of Stirling's formula entails evaluating

$\int_0^\infty \frac{2\arctan (t/z)}{\exp(2 \pi t)-1}\,{\rm d}t = \ln\Gamma (z) - \left( z-\frac12 \right) \ln z +z - \frac12\ln(2\pi).$

One way to do this is by means of a convergent series of inverted rising exponentials. If ; then

$\int_0^\infty \frac{2\arctan (t/z)}{\exp(2 \pi t)-1} \,{\rm d}t = \sum_{n=1}^\infty \frac{c_n}{(z+1)^{\bar n}}$

where

where s(n, k) denotes the Stirling numbers of the first kind. From this we obtain a version of Stirling's series

$\begin{align} \ln \Gamma (z) & = \left( z-\frac12 \right) \ln z -z + \frac{\ln (2 \pi)}{2} \\ & {} + \frac{1}{12(z+1)} + \frac{1}{12(z+1)(z+2)} + \frac{59}{360(z+1)(z+2)(z+3)} \\ & {} + \frac{29}{60(z+1)(z+2)(z+3)(z+4)} + \cdots \end{align}$

which converges when .

Read more about this topic: Stirling's Approximation

Famous quotes containing the words version, stirling and/or formula:

“Exercise is the yuppie version of bulimia.”
—Barbara Ehrenreich (b. 1941)

“Oh, if thy pride did not our joys control,
What world of loving wonders shouldst thou see!
For if I saw thee once transformed in me,
Then in thy bosom I would pour my soul;”
—William Alexander, Earl O Stirling (1580?–1640)

“Hidden away amongst Aschenbach’s writing was a passage directly asserting that nearly all the great things that exist owe their existence to a defiant despite: it is despite grief and anguish, despite poverty, loneliness, bodily weakness, vice and passion and a thousand inhibitions, that they have come into being at all. But this was more than an observation, it was an experience, it was positively the formula of his life and his fame, the key to his work.”
—Thomas Mann (18751955)