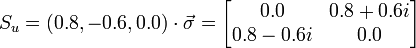Spinors in Three Dimensions - Examples in Physics - Spinors of The Pauli Spin Matrices

Spinors of The Pauli Spin Matrices

See also: quaternions and spatial rotation

Often, the first example of spinors that a student of physics encounters are the 2×1 spinors used in Pauli's theory of electron spin. The Pauli matrices are a vector of three 2×2 matrices that are used as spin operators.

Given a unit vector in 3 dimensions, for example (a, b, c), one takes a dot product with the Pauli spin matrices to obtain a spin matrix for spin in the direction of the unit vector.

The eigenvectors of that spin matrix are the spinors for spin-1/2 oriented in the direction given by the vector.

Example: u = (0.8, -0.6, 0) is a unit vector. Dotting this with the Pauli spin matrices gives the matrix:

The eigenvectors may be found by the usual methods of linear algebra, but a convenient trick is to note that the Pauli spin matrices are square roots of unity, that is, the square of the above matrix is the identity matrix. Thus a (matrix) solution to the eigenvector problem with eigenvalues of ±1 is simply 1 ± S_u. That is,

One can then choose either of the columns of the eigenvector matrix as the vector solution, provided that the column chosen is not zero. Taking the first column of the above, eigenvector solutions for the two eigenvalues are:

The trick used to find the eigenvectors is related to the concept of ideals, that is, the matrix eigenvectors (1 ± S_u)/2 are projection operators or idempotents and therefore each generates an ideal in the Pauli algebra. The same trick works in any Clifford algebra, in particular the Dirac algebra that are discussed below. These projection operators are also seen in density matrix theory where they are examples of pure density matrices.

More generally, the projection operator for spin in the (a, b, c) direction is given by

and any non zero column can be taken as the projection operator. While the two columns appear different, one can use a2 + b2 + c2 = 1 to show that they are multiples (possibly zero) of the same spinor.