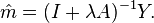Smoothing Spline - Derivation of The Smoothing Spline

Derivation of The Smoothing Spline

It is useful to think of fitting a smoothing spline in two steps:

First, derive the values .
From these values, derive for all x.

Now, treat the second step first.

Given the vector of fitted values, the sum-of-squares part of the spline criterion is fixed. It remains only to minimize, and the minimizer is a natural cubic spline that interpolates the points . This interpolating spline is a linear operator, and can be written in the form

$\hat\mu(x) = \sum_{i=1}^n \hat\mu(x_i) f_i(x)$

where are a set of spline basis functions. As a result, the roughness penalty has the form

$\int \hat\mu''(x)^2 dx = \hat{m}^T A \hat{m}.$

where the elements of A are . The basis functions, and hence the matrix A, depend on the configuration of the predictor variables, but not on the responses or .

Now back to the first step. The penalized sum-of-squares can be written as

$\|Y - \hat m\|^2 + \lambda \hat{m}^T A \hat m,$

where . Minimizing over gives

$\hat m = (I + \lambda A)^{-1} Y.$

Read more about this topic: Smoothing Spline

Famous quotes containing the word smoothing:

“Generation on generation, your neck rubbed the windowsill
of the stall, smoothing the wood as the sea smooths glass.”
—Donald Hall (b. 1928)