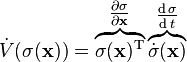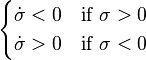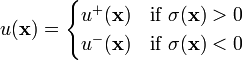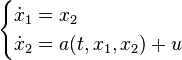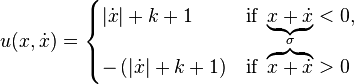Sliding Mode Control - Control Design Examples

Control Design Examples

Consider a plant described by Equation (1) with single input (i.e., ). The switching function is picked to be the linear combination

$\sigma(\mathbf{x}) \triangleq s_1 x_1 + s_2 x_2 + \cdots + s_{n-1} x_{n-1} + s_n x_n$

where the weight for all . The sliding surface is the simplex where . When trajectories are forced to slide along this surface,

and so

which is a reduced-order system (i.e., the new system is of order because the system is constrained to this -dimensional sliding mode simplex). This surface may have favorable properties (e.g., when the plant dynamics are forced to slide along this surface, they move toward the origin ). Taking the derivative of the Lyapunov function in Equation (3), we have

$\dot{V}(\sigma(\mathbf{x})) = \overbrace{\sigma(\mathbf{x})^{\text{T}}}^{\tfrac{\partial \sigma}{\partial \mathbf{x}}} \overbrace{\dot{\sigma}(\mathbf{x})}^{\tfrac{\operatorname{d} \sigma}{\operatorname{d} t}}$

To ensure is a negative-definite function (i.e., for Lyapunov stability of the surface ), the feedback control law must be chosen so that

$\begin{cases} \dot{\sigma} < 0 &\text{if } \sigma > 0\\ \dot{\sigma} > 0 &\text{if } \sigma < 0 \end{cases}$

Hence, the product because it is the product of a negative and a positive number. Note that

$\dot{\sigma}(\mathbf{x}) = \overbrace{\frac{\partial{\sigma(\mathbf{x})}}{\partial{\mathbf{x}}} \dot{\mathbf{x}}}^{\dot{\sigma}(\mathbf{x})} = \frac{\partial{\sigma(\mathbf{x})}}{\partial{\mathbf{x}}} \overbrace{\left( f(\mathbf{x},t) + B(\mathbf{x},t) u \right)}^{\dot{\mathbf{x}}} = \overbrace{}^{\frac{\partial{\sigma(\mathbf{x})}}{\partial{\mathbf{x}}}} \underbrace{\overbrace{\left( f(\mathbf{x},t) + B(\mathbf{x},t) u \right)}^{\dot{\mathbf{x}}}}_{\text{( i.e., an } n \times 1 \text{ vector )}}$

The control law is chosen so that

$u(\mathbf{x}) = \begin{cases} u^+(\mathbf{x}) &\text{if } \sigma(\mathbf{x}) > 0 \\ u^-(\mathbf{x}) &\text{if } \sigma(\mathbf{x}) < 0 \end{cases}$

where

is some control (e.g., possibly extreme, like "on" or "forward") that ensures Equation (5) (i.e., ) is negative at
is some control (e.g., possibly extreme, like "off" or "reverse") that ensures Equation (5) (i.e., ) is positive at

The resulting trajectory should move toward the sliding surface where . Because real systems have delay, sliding mode trajectories often chatter back and forth along this sliding surface (i.e., the true trajectory may not smoothly follow, but it will always return to the sliding mode after leaving it).

Consider the dynamic system

which can be expressed in a 2-dimensional state space (with and ) as

$\begin{cases} \dot{x}_1 = x_2\\ \dot{x}_2 = a(t,x_1,x_2) + u \end{cases}$

Also assume that (i.e., has a finite upper bound that is known). For this system, choose the switching function

By the previous example, we must choose the feedback control law so that . Here,

When (i.e., when ), to make, the control law should be picked so that
When (i.e., when ), to make, the control law should be picked so that

However, by the triangle inequality,

and by the assumption about ,

So the system can be feedback stabilized (to return to the sliding mode) by means of the control law

$u(x,\dot{x}) = \begin{cases} |\dot{x}| + k + 1 &\text{if } \underbrace{x + \dot{x}} < 0,\\ -\left(|\dot{x}| + k + 1\right) &\text{if } \overbrace{x + \dot{x}}^{\sigma} > 0 \end{cases}$

which can be expressed in closed form as

Assuming that the system trajectories are forced to move so that, then

So once the system reaches the sliding mode, the system's 2-dimensional dynamics behave like this 1-dimensional system, which has a globally exponentially stable equilibrium at .

Read more about this topic: Sliding Mode Control

Famous quotes containing the words control, design and/or examples:

“We human beings do have some genuine freedom of choice and therefore some effective control over our own destinies. I am not a determinist. But I also believe that the decisive choice is seldom the latest choice in the series. More often than not, it will turn out to be some choice made relatively far back in the past.”
—A.J. (Arnold Joseph)

“A good scientist is a person with original ideas. A good engineer is a person who makes a design that works with as few original ideas as possible. There are no prima donnas in engineering.”
—Freeman Dyson (b. 1923)

“It is hardly to be believed how spiritual reflections when mixed with a little physics can hold people’s attention and give them a livelier idea of God than do the often ill-applied examples of his wrath.”
—G.C. (Georg Christoph)