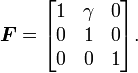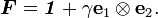Simple Shear in Solid Mechanics
In solid mechanics, a simple shear deformation is defined as an isochoric plane deformation in which there are a set of line elements with a given reference orientation that do not change length and orientation during the deformation. This deformation is differentiated from a pure shear by virtue of the presence of a rigid rotation of the material.
If is the fixed reference orientation in which line elements do not deform during the deformation and is the plane of deformation, then the deformation gradient in simple shear can be expressed as
We can also write the deformation gradient as
Read more about this topic: Simple Shear
Famous quotes containing the words simple, solid and/or mechanics:
“The simple opposition between the people and big business has disappeared because the people themselves have become so deeply involved in big business.”
—Walter Lippmann (1889–1974)
“A building is akin to dogma; it is insolent, like dogma. Whether or no it is permanent, it claims permanence, like a dogma. People ask why we have no typical architecture of the modern world, like impressionism in painting. Surely it is obviously because we have not enough dogmas; we cannot bear to see anything in the sky that is solid and enduring, anything in the sky that does not change like the clouds of the sky.”
—Gilbert Keith Chesterton (1874–1936)
“the moderate Aristotelian city
Of darning and the Eight-Fifteen, where Euclid’s geometry
And Newton’s mechanics would account for our experience,
And the kitchen table exists because I scrub it.”
—W.H. (Wystan Hugh)