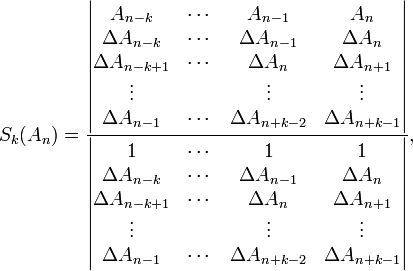Shanks Transformation - Generalized Shanks Transformation

Generalized Shanks Transformation

The generalized kth-order Shanks transformation is given as the ratio of the determinants:

S_k(A_n) = \frac{ \begin{vmatrix} A_{n-k} & \cdots & A_{n-1} & A_n \\ \Delta A_{n-k} & \cdots & \Delta A_{n-1} & \Delta A_{n} \\ \Delta A_{n-k+1} & \cdots & \Delta A_{n} & \Delta A_{n+1} \\ \vdots & & \vdots & \vdots \\ \Delta A_{n-1} & \cdots & \Delta A_{n+k-2} & \Delta A_{n+k-1} \\ \end{vmatrix} }{ \begin{vmatrix} 1 & \cdots & 1 & 1 \\ \Delta A_{n-k} & \cdots & \Delta A_{n-1} & \Delta A_{n} \\ \Delta A_{n-k+1} & \cdots & \Delta A_{n} & \Delta A_{n+1} \\ \vdots & & \vdots & \vdots \\ \Delta A_{n-1} & \cdots & \Delta A_{n+k-2} & \Delta A_{n+k-1} \\ \end{vmatrix} },

with It is the solution of a model for the convergence behaviour of the partial sums with distinct transients:

This model for the convergence behaviour contains unknowns. By evaluating the above equation at the elements and solving for the above expression for the kth-order Shanks transformation is obtained. The first-order generalized Shanks transformation is equal to the ordinary Shanks transformation:

The generalized Shanks transformation is closely related to Padé approximants and Padé tables.

Read more about this topic:  Shanks Transformation

Famous quotes containing the word generalized:

    “One is conscious of no brave and noble earnestness in it, of no generalized passion for intellectual and spiritual adventure, of no organized determination to think things out. What is there is a highly self-conscious and insipid correctness, a bloodless respectability submergence of matter in manner—in brief, what is there is the feeble, uninspiring quality of German painting and English music.”
    —H.L. (Henry Lewis)