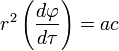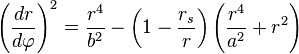Schwarzschild Geodesics - Orbits of Test Particles

Orbits of Test Particles

Dividing both sides by dτ2, the Schwarzschild metric can be rewritten as

$c^{2} = \left( 1 - \frac{r_{s}}{r} \right) c^{2} \left( \frac{dt}{d\tau} \right)^{2} - \frac{1}{1 - \frac{r_{s}}{r}} \left( \frac{dr}{d\tau} \right)^{2} - r^{2} \left( \frac{d\theta}{d\tau} \right)^{2} - r^{2} \sin^{2} \theta \, \left( \frac{d\varphi}{d\tau} \right)^{2},$

The orbit of a particle in this metric is defined by the geodesic equation, which may be solved by any of several methods (as outlined below). This equation yields three constants of motion. First, the motion of the particle is always in a plane, which is equivalent to fixing θ = π/2. The second and third constants of motion, derived below, are taken as two length-scales, a and b, defined by the equations

$\left( 1 - \frac{r_{s}}{r} \right) \left( \frac{dt}{d\tau} \right) = \frac{a}{b}$

$r^{2} \left( \frac{d\varphi}{d\tau} \right) = a c$

where c represents the speed of light. Incorporating these constants of motion into the metric yields the fundamental equation for the particle's orbit

$\left( \frac{dr}{d\varphi} \right)^{2} = \frac{r^{4}}{b^{2}} - \left( 1 - \frac{r_{s}}{r} \right) \left( \frac{r^{4}}{a^{2}} + r^{2} \right)$

Read more about this topic: Schwarzschild Geodesics

Famous quotes containing the words orbits of, orbits, test and/or particles:

“To me, however, the question of the times resolved itself into a practical question of the conduct of life. How shall I live? We are incompetent to solve the times. Our geometry cannot span the huge orbits of the prevailing ideas, behold their return, and reconcile their opposition. We can only obey our own polarity.”
—Ralph Waldo Emerson (1803–1882)

“To me, however, the question of the times resolved itself into a practical question of the conduct of life. How shall I live? We are incompetent to solve the times. Our geometry cannot span the huge orbits of the prevailing ideas, behold their return, and reconcile their opposition. We can only obey our own polarity.”
—Ralph Waldo Emerson (1803–1882)

“I am willing, for a money consideration, to test this physical strength, this nervous force, and muscular power with which I’ve been gifted, to show that they will bear a certain strain. If I break down, if my brain gives way under want of sleep, my heart ceases to respond to the calls made on my circulatory system, or the surcharged veins of my extremities burst—if, in short, I fall helpless, or it may be, dead on the track, then I lose my money.”
—Ada Anderson (1860–?)

“In another’s sentences the thought, though it may be immortal, is as it were embalmed, and does not strike you, but here it is so freshly living, even the body of it not having passed through the ordeal of death, that it stirs in the very extremities, and the smallest particles and pronouns are all alive with it. It is not simply dictionary it, yours or mine, but IT.”
—Henry David Thoreau (1817–1862)