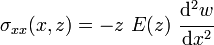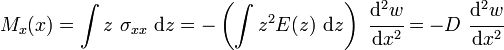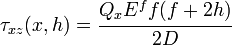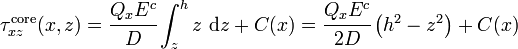Sandwich Theory - Engineering Sandwich Beam Theory

Engineering Sandwich Beam Theory

In the engineering theory of sandwich beams, the axial strain is assumed to vary linearly over the cross-section of the beam as in Euler-Bernoulli theory, i.e.,

$\varepsilon_{xx}(x,z) = -z~\cfrac{\mathrm{d}^2 w}{\mathrm{d} x^2}$

Therefore the axial stress in the sandwich beam is given by

$\sigma_{xx}(x,z) = -z~E(z)~\cfrac{\mathrm{d}^2 w}{\mathrm{d} x^2}$

where is the Young's modulus which is a function of the location along the thickness of the beam. The bending moment in the beam is then given by

$M_x(x) = \int z~\sigma_{xx}~\mathrm{d}z = -\left(\int z^2 E(z)~\mathrm{d}z\right)~\cfrac{\mathrm{d}^2 w}{\mathrm{d} x^2} = -D~\cfrac{\mathrm{d}^2 w}{\mathrm{d} x^2}$

The quantity is called the flexural stiffness of the sandwich beam. The shear force is defined as

$Q_x = \frac{\mathrm{d} M_x}{\mathrm{d} x}~.$

Using these relations, we can show that the stresses in a sandwich beam with a core of thickness and modulus and two facesheets each of thickness and modulus, are given by

$\begin{align} \sigma_{xx}^{\mathrm{f}} & = \cfrac{z E^{\mathrm{f}} M_x}{D} ~;~~ & \sigma_{xx}^{\mathrm{c}} & = \cfrac{z E^{\mathrm{c}} M_x}{D} \\ \tau_{xz}^{\mathrm{f}} & = \cfrac{Q_x E^{\mathrm{f}}}{2D}\left ~;~~ & \tau_{xz}^{\mathrm{c}} & = \cfrac{Q_x}{2D}\left \end{align}$

Derivation of engineering sandwich beam stresses
Since $\cfrac{d^2 w}{d x^2}= -\cfrac{M_x(x)}{D}$ we can write the axial stress as $\sigma_{xx}(x,z) = \cfrac{z~E(z)~M_x(x)}{D}$ The equation of equilibrium for a two-dimensional solid is given by $\frac{\partial \sigma_{xx}}{\partial x} + \frac{\partial \tau_{xz}}{\partial z} = 0$ where is the shear stress. Therefore, $\tau_{xz}(x,z) = \int \frac{\partial \sigma_{xx}}{\partial x}~\mathrm{d}z + C(x) = \int \cfrac{z~E(z)}{D}~\frac{\mathrm{d} M_{x}}{\mathrm{d} x}~\mathrm{d}z + C(x)$ where is a constant of integration. Therefore, $\tau_{xz}(x,z) = \cfrac{Q_x}{D}\int z~E(z)~\mathrm{d}z + C(x)$ Let us assume that there are no shear tractions applied to the top face of the sandwich beam. The shear stress in the top facesheet is given by $\tau^{\mathrm{face}}_{xz}(x,z) = \cfrac{Q_xE^f}{D}\int_z^{h+f} z~\mathrm{d}z + C(x) = \cfrac{Q_x E^f}{2D}\left + C(x)$ At, implies that . Then the shear stress at the top of the core, is given by $\tau_{xz}(x,h) = \cfrac{Q_x E^f f(f+2h)}{2D}$ Similarly, the shear stress in the core can be calculated as $\tau^{\mathrm{core}}_{xz}(x,z) = \cfrac{Q_xE^c}{D}\int_z^{h} z~\mathrm{d}z + C(x) = \cfrac{Q_x E^c}{2D}\left(h^2-z^2\right) + C(x)$ The integration constant is determined from the continuity of shear stress at the interface of the core and the facesheet. Therefore, $C(x) = \cfrac{Q_x E^f f(f+2h)}{2D}$ and $\tau^{\mathrm{core}}_{xz}(x,z) = \cfrac{Q_x}{2D}\left$

Derivation of engineering sandwich beam stresses

Since

$\cfrac{d^2 w}{d x^2}= -\cfrac{M_x(x)}{D}$

we can write the axial stress as

$\sigma_{xx}(x,z) = \cfrac{z~E(z)~M_x(x)}{D}$

The equation of equilibrium for a two-dimensional solid is given by

$\frac{\partial \sigma_{xx}}{\partial x} + \frac{\partial \tau_{xz}}{\partial z} = 0$

where is the shear stress. Therefore,

$\tau_{xz}(x,z) = \int \frac{\partial \sigma_{xx}}{\partial x}~\mathrm{d}z + C(x) = \int \cfrac{z~E(z)}{D}~\frac{\mathrm{d} M_{x}}{\mathrm{d} x}~\mathrm{d}z + C(x)$

where is a constant of integration. Therefore,

$\tau_{xz}(x,z) = \cfrac{Q_x}{D}\int z~E(z)~\mathrm{d}z + C(x)$

Let us assume that there are no shear tractions applied to the top face of the sandwich beam. The shear stress in the top facesheet is given by

$\tau^{\mathrm{face}}_{xz}(x,z) = \cfrac{Q_xE^f}{D}\int_z^{h+f} z~\mathrm{d}z + C(x) = \cfrac{Q_x E^f}{2D}\left + C(x)$

At, implies that . Then the shear stress at the top of the core, is given by

$\tau_{xz}(x,h) = \cfrac{Q_x E^f f(f+2h)}{2D}$

Similarly, the shear stress in the core can be calculated as

$\tau^{\mathrm{core}}_{xz}(x,z) = \cfrac{Q_xE^c}{D}\int_z^{h} z~\mathrm{d}z + C(x) = \cfrac{Q_x E^c}{2D}\left(h^2-z^2\right) + C(x)$

The integration constant is determined from the continuity of shear stress at the interface of the core and the facesheet. Therefore,

$C(x) = \cfrac{Q_x E^f f(f+2h)}{2D}$

and

$\tau^{\mathrm{core}}_{xz}(x,z) = \cfrac{Q_x}{2D}\left$

For a sandwich beam with identical facesheets the value of is

$\begin{align} D & = E^f\int_{-h-f}^{-h} z^2~\mathrm{d}z + E^c\int_{-h}^{h} z^2~\mathrm{d}z + E^f\int_{h}^{h+f} z^2~\mathrm{d}z \\ & = \frac{2}{3}E^ff^3 + \frac{2}{3}E^ch^3 + 2E^ffh(f+h)~. \end{align}$

If, then can be approximated as

$D \approx \frac{2}{3}E^ff^3 + 2E^ffh(f+h) = 2fE^f\left(\frac{1}{3}f^2+h(f+h)\right)$

and the stresses in the sandwich beam can be approximated as

$\begin{align} \sigma_{xx}^{\mathrm{f}} & \approx \cfrac{z M_x}{\frac{2}{3}f^3 +2fh(f+h)} ~;~~ & \sigma_{xx}^{\mathrm{c}} & \approx 0 \\ \tau_{xz}^{\mathrm{f}} & \approx \cfrac{Q_x}{\frac{4}{3}f^3+4fh(f+h)}\left ~;~~ & \tau_{xz}^{\mathrm{c}} & \approx \cfrac{Q_x(f+2h)}{\frac{2}{3}f^2+h(f+h)} \end{align}$

If, in addition, then

$D \approx 2E^ffh(f+h)$

and the approximate stresses in the beam are

$\begin{align} \sigma_{xx}^{\mathrm{f}} & \approx \cfrac{zM_x}{2fh(f+h)} ~;~~& \sigma_{xx}^{\mathrm{c}} & \approx 0 \\ \tau_{xz}^{\mathrm{f}} & \approx \cfrac{Q_x}{4fh(f+h)}\left ~;~~& \tau_{xz}^{\mathrm{c}} & \approx \cfrac{Q_x(f+2h)}{4h(f+h)} \approx \cfrac{Q_x}{2h} \end{align}$

If we assume that the facesheets are thin enough that the stresses may be assumed to be constant through the thickness, we have the approximation

$\begin{align} \sigma_{xx}^{\mathrm{f}} & \approx \pm \cfrac{M_x}{2fh} ~;~~& \sigma_{xx}^{\mathrm{c}} & \approx 0 \\ \tau_{xz}^{\mathrm{f}} & \approx 0 ~;~~ & \tau_{xz}^{\mathrm{c}} & \approx \cfrac{Q_x}{2h} \end{align}$

Hence the problem can be split into two parts, one involving only core shear and the other involving only bending stresses in the facesheets.

Read more about this topic: Sandwich Theory

Famous quotes containing the words engineering, sandwich, beam and/or theory:

“Mining today is an affair of mathematics, of finance, of the latest in engineering skill. Cautious men behind polished desks in San Francisco figure out in advance the amount of metal to a cubic yard, the number of yards washed a day, the cost of each operation. They have no need of grubstakes.”
—Merle Colby, U.S. public relief program (1935-1943)

“As the Sandwich Islander believes that the strength and valor of the enemy he kills passes into himself, so we gain the strength of the temptation we resist.”
—Ralph Waldo Emerson (1803–1882)

“Why beholdest thou the mote that is in thy brother’s eye, but considerest not the beam that is in thine own eye?”
—Bible: New Testament Jesus, in Matthew, 7:3.

From the Sermon on the Mount.

“There is in him, hidden deep-down, a great instinctive artist, and hence the makings of an aristocrat. In his muddled way, held back by the manacles of his race and time, and his steps made uncertain by a guiding theory which too often eludes his own comprehension, he yet manages to produce works of unquestionable beauty and authority, and to interpret life in a manner that is poignant and illuminating.”
—H.L. (Henry Lewis)