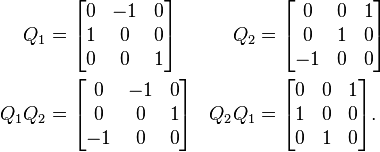Rotation Matrix - Multiplication

Multiplication

The inverse of a rotation matrix is its transpose, which is also a rotation matrix:

The product of two rotation matrices is a rotation matrix:

$\begin{align} (Q_1 Q_2)^T (Q_1 Q_2) &{}= Q_2^T (Q_1^T Q_1) Q_2 = I \\ \det (Q_1 Q_2) &{}= (\det Q_1) (\det Q_2) = +1. \end{align}$

For n greater than 2, multiplication of n×n rotation matrices is not commutative.

$\begin{align} Q_1 &{}= \begin{bmatrix}0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1\end{bmatrix} & Q_2 &{}= \begin{bmatrix}0 & 0 & 1 \\ 0 & 1 & 0 \\ -1 & 0 & 0\end{bmatrix} \\ Q_1 Q_2 &{}= \begin{bmatrix}0 & -1 & 0 \\ 0 & 0 & 1 \\ -1 & 0 & 0\end{bmatrix} & Q_2 Q_1 &{}= \begin{bmatrix}0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0\end{bmatrix}. \end{align}$

Noting that any identity matrix is a rotation matrix, and that matrix multiplication is associative, we may summarize all these properties by saying that the n×n rotation matrices form a group, which for n > 2 is non-abelian. Called a special orthogonal group, and denoted by SO(n), SO(n,R), SO_n, or SO_n(R), the group of n×n rotation matrices is isomorphic to the group of rotations in an n-dimensional space. This means that multiplication of rotation matrices corresponds to composition of rotations, applied in left-to-right order of their corresponding matrices.

Read more about this topic: Rotation Matrix