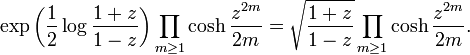Random Permutation Statistics - Permutations That Are Squares

Permutations That Are Squares

Consider what happens when we square a permutation. Fixed points are mapped to fixed points. Odd cycles are mapped to odd cycles in a one-to-one correspondence, e.g. turns into . Even cycles split in two and produce a pair of cycles of half the size of the original cycle, e.g. turns into . Hence permutations that are squares may contain any number of odd cycles, and an even number of cycles of size two, an even number of cycles of size four etc., and are given by

$\mathfrak{P}(\mathfrak{C}_\operatorname{odd}(\mathcal{Z})) \mathfrak{P}_\operatorname{even}(\mathfrak{C}_2(\mathcal{Z})) \mathfrak{P}_\operatorname{even}(\mathfrak{C}_4(\mathcal{Z})) \mathfrak{P}_\operatorname{even}(\mathfrak{C}_6(\mathcal{Z})) \cdots$

which yields the EGF

$\exp \left( \frac{1}{2} \log \frac{1+z}{1-z} \right) \prod_{m\ge 1} \cosh \frac{z^{2m}}{2m} = \sqrt{\frac{1+z}{1-z}} \prod_{m\ge 1} \cosh \frac{z^{2m}}{2m}.$

Read more about this topic: Random Permutation Statistics

Famous quotes containing the words permutations and/or squares:

“The new shopping malls make possible the synthesis of all consumer activities, not least of which are shopping, flirting with objects, idle wandering, and all the permutations of these.”
—Jean Baudrillard (b. 1929)

“And New York is the most beautiful city in the world? It is not far from it. No urban night is like the night there.... Squares after squares of flame, set up and cut into the aether. Here is our poetry, for we have pulled down the stars to our will.”
—Ezra Pound (1885–1972)