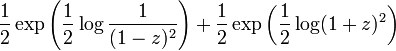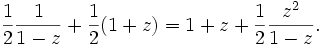Random Permutation Statistics - Number of Permutations Containing An Even Number of Even Cycles

Number of Permutations Containing An Even Number of Even Cycles

We may use the Flajolet–Sedgewick fundamental theorem directly and compute more advanced permutation statistics. (Check that page for an explanation of how the operators we will use are computed.) For example, the set of permutations containing an even number of even cycles is given by

$\mathfrak{P}(\mathfrak{C}_{\operatorname{odd}}(\mathcal{Z})) \mathfrak{P}_{\operatorname{even}}(\mathfrak{C}_{\operatorname{even}}(\mathcal{Z})).$

Translating to exponential generating functions (EGFs), we obtain

$\exp \left( \frac{1}{2} \log \frac{1+z}{1-z} \right) \cosh \left( \frac{1}{2} \log \frac{1}{1-z^2} \right)$

$\frac{1}{2} \exp \left( \frac{1}{2} \left( \log \frac{1+z}{1-z} + \log \frac{1}{1-z^2} \right) \right) + \frac{1}{2} \exp \left( \frac{1}{2} \left( \log \frac{1+z}{1-z} - \log \frac{1}{1-z^2} \right) \right).$

This simplifies to

$\frac{1}{2} \exp \left( \frac{1}{2} \log \frac{1}{(1-z)^2} \right) + \frac{1}{2} \exp \left( \frac{1}{2} \log (1+z)^2 \right)$

$\frac{1}{2} \frac{1}{1-z} + \frac{1}{2} (1+z) = 1 + z + \frac{1}{2} \frac{z^2}{1-z}.$

This says that there is one permutation of size zero containing an even number of even cycles (the empty permutation, which contains zero cycles of even length), one such permutation of size one (the fixed point, which also contains zero cycles of even length), and that for, there are such permutations.

Read more about this topic: Random Permutation Statistics

Famous quotes containing the words number of, number, permutations and/or cycles:

“I can’t quite define my aversion to asking questions of strangers. From snatches of family battles which I have heard drifting up from railway stations and street corners, I gather that there are a great many men who share my dislike for it, as well as an equal number of women who ... believe it to be the solution to most of this world’s problems.”
—Robert Benchley (1889–1945)

“The growing good of the world is partly dependent on unhistoric acts; and that things are not so ill with you and me as they might have been, is half owing to the number who lived faithfully a hidden life, and rest in unvisited tombs.”
—George Eliot [Mary Ann (or Marian)

“Motherhood in all its guises and permutations is more art than science.”
—Melinda M. Marshall (20th century)

“The stars which shone over Babylon and the stable in Bethlehem still shine as brightly over the Empire State Building and your front yard today. They perform their cycles with the same mathematical precision, and they will continue to affect each thing on earth, including man, as long as the earth exists.”
—Linda Goodman (b. 1929)