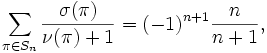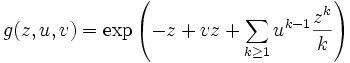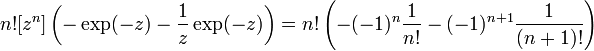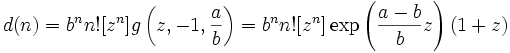Random Permutation Statistics - A Problem From The 2005 Putnam Competition

A Problem From The 2005 Putnam Competition

A link to the Putnam competition website appears in the section External links. The problem asks for a proof that

$\sum_{\pi\in S_n} \frac{\sigma(\pi)}{\nu(\pi)+1} = (-1)^{n+1} \frac{n}{n+1},$

where the sum is over all permutations of, is the sign of, i.e. if is even and if is odd, and is the number of fixed points of .

Now the sign of is given by

where the product is over all cycles c of, as explained e.g. on the page on even and odd permutations.

Hence we consider the combinatorial class

$\mathfrak{P}( - \mathcal{Z} + \mathcal{V} \mathcal{Z} + \mathfrak{C}_1(\mathcal{Z}) + \mathcal{U}\mathfrak{C}_2(\mathcal{Z}) + \mathcal{U}^2\mathfrak{C}_3(\mathcal{Z}) + \mathcal{U}^3\mathfrak{C}_4(\mathcal{Z}) + \cdots)$

where marks one minus the length of a contributing cycle, and marks fixed points. Translating to generating functions, we obtain

$g(z, u, v) = \exp\left( -z + vz + \sum_{k\ge 1} u^{k-1} \frac{z^k}{k} \right)$

$\exp\left( -z + vz + \frac{1}{u} \log\frac{1}{1-uz} \right) = \exp(-z + vz) \left(\frac{1}{1-uz} \right)^{1/u}.$

Now we have

$n! g(z, -1, v) = n! \exp(-z + vz) (1 + z) = \sum_{\pi\in S_n} \sigma(\pi) v^{\nu(\pi)}$

and hence the desired quantity is given by

$n! \int_0^1 g(z, -1, v) dv = \sum_{\pi\in S_n} \frac{\sigma(\pi)}{\nu(\pi)+1}.$

Doing the computation, we obtain

$\int_0^1 g(z, -1, v) dv = \exp(-z)(1+z) \left(\frac{1}{z}\exp(z) - \frac{1}{z}\right)$

$\left(\frac{1}{z} + 1\right) \left(1 - \exp(-z)\right) = \frac{1}{z} + 1 - \exp(-z) - \frac{1}{z} \exp(-z).$

Extracting coefficients, we find that the coefficient of is zero. The constant is one, which does not agree with the formula (should be zero). For positive, however, we obtain

$n! \left( - \exp(-z) - \frac{1}{z} \exp(-z) \right) = n! \left( - (-1)^n \frac{1}{n!} - (-1)^{n+1} \frac{1}{(n+1)!} \right)$

$(-1)^{n+1} \left( 1 - \frac{1}{n+1} \right) = (-1)^{n+1} \frac{n}{n+1},$

which is the desired result.

As an interesting aside, we observe that may be used to evaluate the following determinant of an matrix:

$d(n) = \det(A_n) = \begin{vmatrix} a && b && b && \cdots && b \\ b && a && b && \cdots && b \\ b && b && a && \cdots && b \\ \vdots && \vdots && \vdots && \ddots && \vdots \\ b && b && b && \cdots && a \end{vmatrix}.$

where . Recall the formula for the determinant:

Now the value of the product on the right for a permutation is, where f is the number of fixed points of . Hence

$d(n) = b^n n! g\left(z, -1, \frac{a}{b}\right)= b^n n! \exp \left(\frac{a-b}{b} z\right) (1+z)$

which yields

$b^n \left(\frac{a-b}{b}\right)^n + b^n n \left(\frac{a-b}{b}\right)^{n-1} = (a-b)^n + n b (a-b)^{n-1}$

and finally

Read more about this topic: Random Permutation Statistics

Famous quotes containing the words problem, putnam and/or competition:

“I tell you, sir, the only safeguard of order and discipline in the modern world is a standardized worker with interchangeable parts. That would solve the entire problem of management.”
—Jean Giraudoux (1882–1944)

“Cut the pie any way you like, “meanings” just ain’t in the head!”
—Hilary Putnam (b. 1926)

“Knowledge in the form of an informational commodity indispensable to productive power is already, and will continue to be, a major—perhaps the major—stake in the worldwide competition for power. It is conceivable that the nation-states will one day fight for control of information, just as they battled in the past for control over territory, and afterwards for control over access to and exploitation of raw materials and cheap labor.”
—Jean François Lyotard (b. 1924)