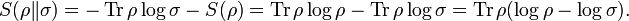Quantum Relative Entropy - Definition

Definition

As with many other objects in quantum information theory, quantum relative entropy is defined by extending the classical definition from probability distributions to density matrices. Let ρ be a density matrix. The von Neumann entropy of ρ, which is the quantum mechanical analog of the Shannon entropy, is given by

For two density matrices ρ and σ, the quantum relative entropy of ρ with respect to σ is defined by

S(\rho \| \sigma) = - \operatorname{Tr} \rho \log \sigma - S(\rho) = \operatorname{Tr} \rho \log \rho - \operatorname{Tr} \rho \log \sigma = \operatorname{Tr}\rho (\log \rho - \log \sigma).

We see that, when the states are classical, i.e. ρσ = σρ, the definition coincides with the classical case.

Read more about this topic:  Quantum Relative Entropy

Famous quotes containing the word definition:

    “Was man made stupid to see his own stupidity?
    Is God by definition indifferent, beyond us all?
    Is the eternal truth man’s fighting soul
    Wherein the Beast ravens in its own avidity?”
    —Richard Eberhart (b. 1904)

    “The definition of good prose is proper words in their proper places; of good verse, the most proper words in their proper places. The propriety is in either case relative. The words in prose ought to express the intended meaning, and no more; if they attract attention to themselves, it is, in general, a fault.”
    —Samuel Taylor Coleridge (1772–1834)

    “... if, as women, we accept a philosophy of history that asserts that women are by definition assimilated into the male universal, that we can understand our past through a male lens—if we are unaware that women even have a history—we live our lives similarly unanchored, drifting in response to a veering wind of myth and bias.”
    —Adrienne Rich (b. 1929)