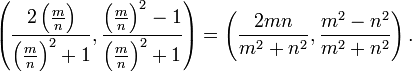Geometry of Euclid's Formula
Euclid's formulae for a Pythagorean triple
can be understood in terms of the geometry of rational number points on the unit circle (Trautman 1998). To motivate this, consider a right triangle with legs a and b, and hypotenuse c, where a, b, and c are positive integers. By the Pythagorean theorem, a2 + b2 = c2 or, dividing both sides by c2,
Geometrically, the point in the Cartesian plane with coordinates
is on the unit circle x2 + y2 = 1. In this equation, the coordinates x and y are given by rational numbers. Conversely, any point on the unit circle whose coordinates x, y are rational numbers gives rise to a primitive Pythagorean triple. Indeed, write x and y as fractions in lowest terms:
where the greatest common divisor of a, b, and c is 1. Then, since x and y are on the unit circle,
as claimed.
There is therefore a correspondence between points on the unit circle with rational coordinates and primitive Pythagorean triples. At this point, Euclid's formulae can be derived either by methods of trigonometry or equivalently by using the stereographic projection.
For the stereographic approach, suppose that P′ is a point on the x-axis with rational coordinates P′(m/n,0). Then, it can be shown by basic algebra that the point P has coordinates
This establishes that each rational point of the x-axis goes over to a rational point of the unit circle. The converse, that every rational point of the unit circle comes from such a point of the x-axis, follows by applying the inverse stereographic projection. Suppose that P(x, y) is a point of the unit circle with x and y rational numbers. Then the point P′ obtained by stereographic projection onto the x-axis has coordinates
which is rational.
In terms of algebraic geometry, the algebraic variety of rational points on the unit circle is birational to the affine line over the rational numbers. The unit circle is thus called a rational curve, and it is this fact which enables an explicit parameterization of the (rational number) points on it by means of rational functions.
Read more about this topic: Pythagorean Triple
Famous quotes containing the words geometry of, geometry and/or formula:
“The geometry of landscape and situation seems to create its own systems of time, the sense of a dynamic element which is cinematising the events of the canvas, translating a posture or ceremony into dynamic terms. The greatest movie of the 20th century is the Mona Lisa, just as the greatest novel is Gray’s Anatomy.”
—J.G. (James Graham)
“... geometry became a symbol for human relations, except that it was better, because in geometry things never go bad. If certain things occur, if certain lines meet, an angle is born. You cannot fail. It’s not going to fail; it is eternal. I found in rules of mathematics a peace and a trust that I could not place in human beings. This sublimation was total and remained total. Thus, I’m able to avoid or manipulate or process pain.”
—Louise Bourgeois (b. 1911)
“So, if we must give a general formula applicable to all kinds of soul, we must describe it as the first actuality [entelechy] of a natural organized body.”
—Aristotle (384–323 B.C.)