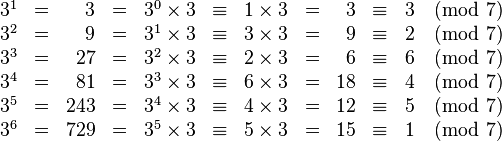Primitive Root Modulo n - Elementary Example

Elementary Example

The number 3 is a primitive root modulo 7 because

\begin{array}{rcrcrcrcrcr} 3^1 &=& 3 &=& 3^0 \times 3 &\equiv& 1 \times 3 &=& 3 &\equiv& 3 \pmod 7 \\ 3^2 &=& 9 &=& 3^1 \times 3 &\equiv& 3 \times 3 &=& 9 &\equiv& 2 \pmod 7 \\ 3^3 &=& 27 &=& 3^2 \times 3 &\equiv& 2 \times 3 &=& 6 &\equiv& 6 \pmod 7 \\ 3^4 &=& 81 &=& 3^3 \times 3 &\equiv& 6 \times 3 &=& 18 &\equiv& 4 \pmod 7 \\ 3^5 &=& 243 &=& 3^4 \times 3 &\equiv& 4 \times 3 &=& 12 &\equiv& 5 \pmod 7 \\ 3^6 &=& 729 &=& 3^5 \times 3 &\equiv& 5 \times 3 &=& 15 &\equiv& 1 \pmod 7 \\ \end{array}

Here we see that the period of 3k modulo 7 is 6. The remainders in the period, which are 3, 2, 6, 4, 5, 1, form a rearrangement of all nonzero remainders modulo 7, implying that 3 is indeed a primitive root modulo 7. Curiously, permutations created in this way (and their circular shifts) have been shown to be Costas arrays.

Read more about this topic:  Primitive Root Modulo n

Famous quotes containing the word elementary:

    “When the Devil quotes Scriptures, it’s not, really, to deceive, but simply that the masses are so ignorant of theology that somebody has to teach them the elementary texts before he can seduce them.”
    —Paul Goodman (1911–1972)

    “Listen. We converse as we live—by repeating, by combining and recombining a few elements over and over again just as nature does when of elementary particles it builds a world.”
    —William Gass (b. 1924)