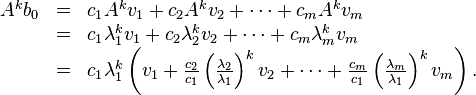Power Iteration - Analysis

Analysis

Let be decomposed into its Jordan canonical form:, where the first column of is an eigenvector of corresponding to the dominant eigenvalue . Since the dominant eigenvalue of is unique, the first Jordan block of is the matrix, where is the largest eigenvalue of A in magnitude. The starting vector can be written as a linear combination of the columns of V: . By assumption, has a nonzero component in the direction of the dominant eigenvalue, so .

The computationally useful recurrence relation for can be rewritten as:, where the expression: is more amenable to the following analysis.
\displaystyle \begin{array}{lcl} b_{k} &=& \frac{A^{k}b_{0}}{\| A^{k} b_{0} \|} \\ &=& \frac{\left( VJV^{-1} \right)^{k} b_{0}}{\|\left( VJV^{-1} \right)^{k}b_{0}\|} \\ &=& \frac{ VJ^{k}V^{-1} b_{0}}{\| V J^{k} V^{-1} b_{0}\|} \\ &=& \frac{ VJ^{k}V^{-1} \left( c_{1}v_{1} + c_{2}v_{2} + \cdots + c_{n}v_{n} \right)} {\| V J^{k} V^{-1} \left( c_{1}v_{1} + c_{2}v_{2} + \cdots + c_{n}v_{n} \right)\|} \\ &=& \frac{ VJ^{k}\left( c_{1}e_{1} + c_{2}e_{2} + \cdots + c_{n}e_{n} \right)} {\| V J^{k} \left( c_{1}e_{1} + c_{2}e_{2} + \cdots + c_{n}e_{n} \right) \|} \\ &=& \left( \frac{\lambda_{1}}{|\lambda_{1}|} \right)^{k} \frac{c_{1}}{|c_{1}|} \frac{ v_{1} + \frac{1}{c_{1}} V \left( \frac{1}{\lambda_1} J \right)^{k} \left( c_{2}e_{2} + \cdots + c_{n}e_{n} \right)} {\| v_{1} + \frac{1}{c_{1}} V \left( \frac{1}{\lambda_1} J \right)^{k} \left( c_{2}e_{2} + \cdots + c_{n}e_{n} \right) \| } \end{array}
The expression above simplifies as
\left( \frac{1}{\lambda_{1}} J \right)^{k} = \begin{bmatrix} & & & & \\ & \left( \frac{1}{\lambda_{1}} J_{2} \right)^{k}& & & \\ & & \ddots & \\ & & & \left( \frac{1}{\lambda_{1}} J_{m} \right)^{k} \\ \end{bmatrix} \rightarrow \begin{bmatrix} 1 & & & & \\ & 0 & & & \\ & & \ddots & \\ & & & 0 \\ \end{bmatrix} as .
The limit follows from the fact that the eigenvalue of is less than 1 in magnitude, so \left( \frac{1}{\lambda_{1}} J_{i} \right)^{k} \rightarrow 0 as
It follows that:
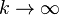
\frac{1}{c_{1}} V \left( \frac{1}{\lambda_1} J \right)^{k} \left( c_{2}e_{2} + \cdots + c_{n}e_{n} \right) \rightarrow 0 as k \rightarrow \infty
Using this fact, can be written in a form that emphasizes its relationship with when k is large:
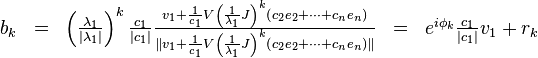\begin{matrix} b_{k} &=& \left( \frac{\lambda_{1}}{|\lambda_{1}|} \right)^{k} \frac{c_{1}}{|c_{1}|} \frac{ v_{1} + \frac{1}{c_{1}} V \left( \frac{1}{\lambda_1} J \right)^{k} \left( c_{2}e_{2} + \cdots + c_{n}e_{n} \right)} {\| v_{1} + \frac{1}{c_{1}} V \left( \frac{1}{\lambda_1} J \right)^{k} \left( c_{2}e_{2} + \cdots + c_{n}e_{n} \right) \| } &=& e^{i \phi_{k}} \frac{c_{1}}{|c_{1}|} v_{1} + r_{k} \end{matrix} where and as
The sequence is bounded, so it contains a convergent subsequence. Note that the eigenvector corresponding to the dominant eigenvalue is only unique up to a scalar, so although the sequence may not converge, is nearly an eigenvector of A for large k.

Alternatively, if A is diagonalizable, then the following proof yields the same result
Let λ1, λ2, …, λm be the m eigenvalues (counted with multiplicity) of A and let v1, v2, …, vm be the corresponding eigenvectors. Suppose that is the dominant eigenvalue, so that for .

The initial vector can be written:

If is chosen randomly (with uniform probability), then c1 ≠ 0 with probability 1. Now,

\begin{array}{lcl}A^{k}b_0 & = & c_{1}A^{k}v_{1} + c_{2}A^{k}v_{2} + \cdots + c_{m}A^{k}v_{m} \\ & = & c_{1}\lambda_{1}^{k}v_{1} + c_{2}\lambda_{2}^{k}v_{2} + \cdots + c_{m}\lambda_{m}^{k}v_{m} \\ & = & c_{1}\lambda_{1}^{k} \left( v_{1} + \frac{c_{2}}{c_{1}}\left(\frac{\lambda_{2}}{\lambda_{1}}\right)^{k}v_{2} + \cdots + \frac{c_{m}}{c_{1}}\left(\frac{\lambda_{m}}{\lambda_{1}}\right)^{k}v_{m}\right). \end{array}

The expression within parentheses converges to because for . On the other hand, we have

Therefore, converges to (a multiple of) the eigenvector . The convergence is geometric, with ratio

where denotes the second dominant eigenvalue. Thus, the method converges slowly if there is an eigenvalue close in magnitude to the dominant eigenvalue.

Read more about this topic:  Power Iteration

Famous quotes containing the word analysis:

    “Ask anyone committed to Marxist analysis how many angels on the head of a pin, and you will be asked in return to never mind the angels, tell me who controls the production of pins.”
    —Joan Didion (b. 1934)

    “Cubism had been an analysis of the object and an attempt to put it before us in its totality; both as analysis and as synthesis, it was a criticism of appearance. Surrealism transmuted the object, and suddenly a canvas became an apparition: a new figuration, a real transfiguration.”
    —Octavio Paz (b. 1914)

    “Whatever else American thinkers do, they psychologize, often brilliantly. The trouble is that psychology only takes us so far. The new interest in families has its merits, but it will have done us all a disservice if it turns us away from public issues to private matters. A vision of things that has no room for the inner life is bankrupt, but a psychology without social analysis or politics is both powerless and very lonely.”
    —Joseph Featherstone (20th century)