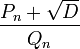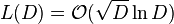Periodic Continued Fraction - Length of The Repeating Block

Length of The Repeating Block

By analyzing the sequence of combinations

\frac{P_n + \sqrt{D}}{Q_n}

that can possibly arise when ζ = (P + √D)/Q is expanded as a regular continued fraction, Lagrange showed that the largest partial denominator ai in the expansion is less than 2√D, and that the length of the repeating block is less than 2D.

More recently, sharper arguments based on the divisor function have shown that L(D), the length of the repeating block for a quadratic surd of discriminant D, is given by

L(D) = \mathcal{O}(\sqrt{D}\ln{D})

where the big O means "on the order of", or "asymptotically proportional to" (see big O notation).

Read more about this topic:  Periodic Continued Fraction

Famous quotes containing the words length of, length, repeating and/or block:

    “To find the length of an object, we have to perform certain
    physical operations. The concept of length is therefore fixed when the operations by which length is measured are fixed: that is, the concept of length involves as much as and nothing more than the set of operations by which length is determined.”
    —Percy W. Bridgman (1882–1961)

    “We praise a man who feels angry on the right grounds and against the right persons and also in the right manner at the right moment and for the right length of time.”
    —Aristotle (384–322 B.C.)

    “Anytime we react to behavior in our children that we dislike in ourselves, we need to proceed with extreme caution. The dynamics of everyday family life also have a way of repeating themselves.”
    —Cathy Rindner Tempelsman (20th century)

    “Of course I lie to people. But I lie altruistically—for our mutual good. The lie is the basic building block of good manners. That may seem mildly shocking to a moralist—but then what isn’t?”
    —Quentin Crisp (b. 1908)