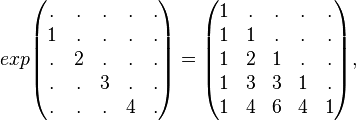Pascal's Triangle - Extensions

Extensions

Pascal's Triangle can be extended to negative row numbers.

First write the triangle in the following form:

m = 0 m = 1 m = 2 m = 3 m = 4 m = 5 ...
n = 0 1 0 0 0 0 0 ...
n = 1 1 1 0 0 0 0 ...
n = 2 1 2 1 0 0 0 ...
n = 3 1 3 3 1 0 0 ...
n = 4 1 4 6 4 1 0 ...

Next, extend the column of 1s upwards:

m = 0 m = 1 m = 2 m = 3 m = 4 m = 5 ...
n = −4 1 ...
n = −3 1 ...
n = −2 1 ...
n = −1 1 ...
n = 0 1 0 0 0 0 0 ...
n = 1 1 1 0 0 0 0 ...
n = 2 1 2 1 0 0 0 ...
n = 3 1 3 3 1 0 0 ...
n = 4 1 4 6 4 1 0 ...

Now the rule:

can be rearranged to:

which allows calculation of the other entries for negative rows:

m = 0 m = 1 m = 2 m = 3 m = 4 m = 5 ...
n = −4 1 −4 10 −20 35 −56 ...
n = −3 1 −3 6 −10 15 −21 ...
n = −2 1 −2 3 −4 5 −6 ...
n = −1 1 −1 1 −1 1 −1 ...
n = 0 1 0 0 0 0 0 ...
n = 1 1 1 0 0 0 0 ...
n = 2 1 2 1 0 0 0 ...
n = 3 1 3 3 1 0 0 ...
n = 4 1 4 6 4 1 0 ...

This extension preserves the property that the values in the mth column viewed as a function of n are fit by an order m polynomial, namely

{n \choose m} = \frac{1}{m!}\prod_{k=0}^{m-1} (n-k) = \frac{1}{m!}\prod_{k=1}^{m} (n-k+1) .

This extension also preserves the property that the values in the nth row correspond to the coefficients of :

(1+x)^n = \sum_{k=0}^\infty {n \choose k} x^k \quad |x| < 1

For example:

(1+x)^{-2} = 1-2x+3x^2-4x^3+\cdots \quad |x| < 1

Another option for extending Pascal's triangle to negative rows comes from extending the other line of 1s:

m = −4 m = −3 m = −2 m = −1 m = 0 m = 1 m = 2 m = 3 m = 4 m = 5 ...
n = −4 1 0 0 0 0 0 0 0 0 0 ...
n = −3 1 0 0 0 0 0 0 0 0 ...
n = −2 1 0 0 0 0 0 0 0 ...
n = −1 1 0 0 0 0 0 0 ...
n = 0 0 0 0 0 1 0 0 0 0 0 ...
n = 1 0 0 0 0 1 1 0 0 0 0 ...
n = 2 0 0 0 0 1 2 1 0 0 0 ...
n = 3 0 0 0 0 1 3 3 1 0 0 ...
n = 4 0 0 0 0 1 4 6 4 1 0 ...

Applying the same rule as before leads to

m = −4 m = −3 m = −2 m = −1 m = 0 m = 1 m = 2 m = 3 m = 4 m = 5 ...
n = −4 1 0 0 0 0 0 0 0 0 0 ...
n = −3 −3 1 0 0 0 0 0 0 0 0 ...
n = −2 3 −2 1 0 0 0 0 0 0 0 ...
n = −1 −1 1 −1 1 0 0 0 0 0 0 ..
n = 0 0 0 0 0 1 0 0 0 0 0 ...
n = 1 0 0 0 0 1 1 0 0 0 0 ...
n = 2 0 0 0 0 1 2 1 0 0 0 ...
n = 3 0 0 0 0 1 3 3 1 0 0 ...
n = 4 0 0 0 0 1 4 6 4 1 0 ...

Note that this extension also has the properties that just as

exp\begin{pmatrix} . & . & . & . & . \\ 1 & . & . & . & . \\ . & 2 & . & . & . \\ . & . & 3 & . & . \\ . & . & . & 4 & . \end{pmatrix} = \begin{pmatrix} 1 & . & . & . & . \\ 1 & 1 & . & . & . \\ 1 & 2 & 1 & . & . \\ 1 & 3 & 3 & 1 & . \\ 1 & 4 & 6 & 4 & 1 \end{pmatrix},

we have

exp\begin{pmatrix} . & . & . & . & . & . & . & . & . & . \\ -4 & . & . & . & . & . & . & . & . & . \\ . & -3 & . & . & . & . & . & . & . & . \\ . & . & -2 & . & . & . & . & . & . & . \\ . & . & . & -1 & . & . & . & . & . & . \\ . & . & . & . & 0 & . & . & . & . & . \\ . & . & . & . & . & 1 & . & . & . & . \\ . & . & . & . & . & . & 2 & . & . & . \\ . & . & . & . & . & . & . & 3 & . & . \\ . & . & . & . & . & . & . & . & 4 & . \end{pmatrix} = \begin{pmatrix} 1 & . & . & . & . & . & . & . & . & . \\ -4 & 1 & . & . & . & . & . & . & . & . \\ 6 & -3 & 1 & . & . & . & . & . & . & . \\ -4 & 3 & -2 & 1 & . & . & . & . & . & . \\ 1 & -1 & 1 & -1 & 1 & . & . & . & . & . \\ . & . & . & . & . & 1 & . & . & . & . \\ . & . & . & . & . & 1 & 1 & . & . & . \\ . & . & . & . & . & 1 & 2 & 1 & . & . \\ . & . & . & . & . & 1 & 3 & 3 & 1 & . \\ . & . & . & . & . & 1 & 4 & 6 & 4 & 1 \end{pmatrix}

Also, just as summing along the lower-left to upper-right diagonals of the Pascal matrix yields the Fibonacci numbers, this second type of extension still sums to the Fibonacci numbers for negative index.

Either of these extensions can be reached if we define

and take certain limits of the Gamma function, .

Read more about this topic:  Pascal's Triangle

Famous quotes containing the word extensions:

    “The psychological umbilical cord is more difficult to cut than the real one. We experience our children as extensions of ourselves, and we feel as though their behavior is an expression of something within us...instead of an expression of something in them. We see in our children our own reflection, and when we don’t like what we see, we feel angry at the reflection.”
    —Elaine Heffner (20th century)

    “If we focus exclusively on teaching our children to read, write, spell, and count in their first years of life, we turn our homes into extensions of school and turn bringing up a child into an exercise in curriculum development. We should be parents first and teachers of academic skills second.”
    —Neil Kurshan (20th century)