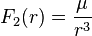Newton's Theorem of Revolving Orbits - Illustrative Example: Cotes' Spirals

Illustrative Example: Cotes' Spirals

The simplest illustration of Newton's theorem occurs when there is no initial force, i.e., F₁(r) = 0. In this case, the first particle is stationary or travels in a straight line. If it travels in a straight line that does not pass through the origin (blue line in Figure 6) the equation for such a line may be written in the polar coordinates (r, θ₁) as

$\frac{1}{r} = \frac{1}{b} \cos\ (\theta_1 - \theta_0)$

where θ₀ is the angle at which the distance is minimized (Figure 6). The distance r begins at infinity (when θ₁ – θ₀ = −90°), and decreases gradually until θ₁ – θ₀ = 0°, when the distance reaches a minimum, then gradually increases again to infinity at θ₁ – θ₀ = 90°. The minimum distance b is the impact parameter, which is defined as the length of the perpendicular from the fixed center to the line of motion. The same radial motion is possible when an inverse-cube central force is added.

An inverse-cube central force F₂(r) has the form

$F_2(r) = \frac{\mu}{r^3}$

where the numerator μ may be positive (repulsive) or negative (attractive). If such an inverse-cube force is introduced, Newton's theorem says that the corresponding solutions have a shape called Cotes' spirals. These are curves defined by the equation

$\frac{1}{r} = \frac{1}{b} \cos\ \left(\frac{\theta_2 - \theta_0}{k} \right)$

where the constant k equals

$k^2 = 1 - \frac{m \mu}{L_1^2}$

When the right-hand side of the equation is a positive real number, the solution corresponds to an epispiral. When the argument θ₁ – θ₀ equals ±90°×k, the cosine goes to zero and the radius goes to infinity. Thus, when k is less than one, the range of allowed angles becomes small and the force is repulsive (red curve on right in Figure 7). On the other hand, when k is greater than one, the range of allowed angles increases, corresponding to an attractive force (green, cyan and blue curves on left in Figure 7); the orbit of the particle can even wrap around the center several times. The possible values of the parameter k may range from zero to infinity, which corresponds to values of μ ranging from negative infinity up to the positive upper limit, L₁2/m. Thus, for all attractive inverse-cube forces (negative μ) there is a corresponding epispiral orbit, as for some repulsive ones (μ < L₁2/m), as illustrated in Figure 7. Stronger repulsive forces correspond to a faster linear motion.

One of the other solution types is given in terms of the hyperbolic cosine:

$\frac{1}{r} = \frac{1}{b} \cosh\ \left(\frac{\theta_0 - \theta_2}{\lambda} \right)$

where the constant λ satisfies

$\lambda^2 = \frac{m \mu}{L_1^{2}} - 1$

This form of Cotes' spirals corresponds to one of the two Poinsot's spirals (Figure 8). The possible values of λ range from zero to infinity, which corresponds to values of μ greater than the positive number L₁2/m. Thus, Poinsot spiral motion only occurs for repulsive inverse-cube central forces, and applies in the case that L is not too large for the given μ.

Taking the limit of k or λ going to zero yields the third form of a Cotes' spiral, the so-called reciprocal spiral or hyperbolic spiral, as a solution

$\frac{1}{r} = A \theta_2 + \varepsilon$

where A and ε are arbitrary constants. Such curves result when the strength μ of the repulsive force exactly balances the angular momentum-mass term

$\mu = \frac{L_{1}^{2}}{m}$

Read more about this topic: Newton's Theorem Of Revolving Orbits