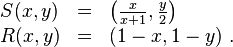Minkowski's Question Mark Function

Self-symmetry

The question mark is clearly visually self-similar. A monoid of self-similarities may be generated by two operators S and R acting on the unit square and defined as follows:

$\begin{array}{lcl} S(x, y) &=& \left( \frac{x}{x+1}, \frac{y}{2} \right) \\ R(x, y) &=& \left( 1-x, 1-y \right)\,. \end{array}$

Visually, S shrinks the unit square to its bottom-left quarter, while R performs a point reflection through its center.

A point on the graph of ? has coordinates (x, ?(x)) for some x in the unit interval. Such a point is transformed by S and R into another point of the graph, because ? satisfies the following identities for all :

$\begin{array}{lcl} ?\left(\frac{x}{x+1}\right) &=& \frac{?(x)}{2} \\ ?(1-x) &=& 1-?(x)\,. \end{array}$

These two operators may be repeatedly combined, forming a monoid. A general element of the monoid is then

for positive integers . Each such element describes a self-similarity of the question mark function. This monoid is sometimes called the period-doubling monoid, and all period-doubling fractal curves have a self-symmetry described by it (the de Rham curve, of which the question mark is a special case, is a category of such curves). Note also that the elements of the monoid are in correspondence with the rationals, by means of the identification of with the continued fraction . Since both

and

are linear fractional transformations with integer coefficients, the monoid may be regarded as a subset of the modular group PSL(2,Z).

Read more about this topic: Minkowski's Question Mark Function

Minkowski's Question Mark Function - Self-symmetry