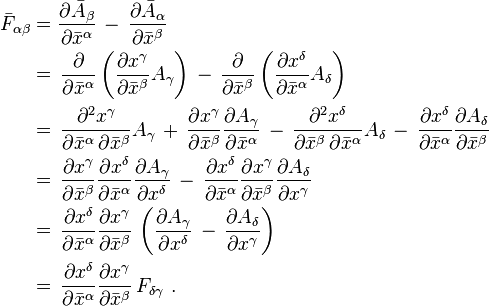Maxwell's Equations in Curved Spacetime - Electromagnetic Field

Electromagnetic Field

The electromagnetic field is a covariant antisymmetric tensor of rank 2 which can be defined in terms of the electromagnetic potential by

To see that this equation is invariant, we transform the coordinates (as described in the classical treatment of tensors)

\begin{align} \bar{F}_{\alpha \beta} & = \frac{\partial \bar{A}_{\beta}}{\partial \bar{x}^{\alpha}} \, - \, \frac{\partial \bar{A}_{\alpha}}{\partial \bar{x}^{\beta}} \\ & = \, \frac{\partial}{\partial \bar{x}^{\alpha}} \left( \frac{\partial x^{\gamma}}{\partial \bar{x}^{\beta}} A_{\gamma} \right) \, - \, \frac{\partial}{\partial \bar{x}^{\beta}} \left( \frac{\partial x^{\delta}}{\partial \bar{x}^{\alpha}} A_{\delta} \right) \\ & = \, \frac{\partial^2 x^{\gamma}}{\partial \bar{x}^{\alpha} \, \partial \bar{x}^{\beta}} A_{\gamma} \, + \, \frac{\partial x^{\gamma}}{\partial \bar{x}^{\beta}} \frac{\partial A_{\gamma}}{\partial \bar{x}^{\alpha}} \, - \, \frac{\partial^2 x^{\delta}}{\partial \bar{x}^{\beta} \, \partial \bar{x}^{\alpha}} A_{\delta} \, - \, \frac{\partial x^{\delta}}{\partial \bar{x}^{\alpha}} \frac{\partial A_{\delta}}{\partial \bar{x}^{\beta}} \\ & = \, \frac{\partial x^{\gamma}}{\partial \bar{x}^{\beta}} \frac{\partial x^{\delta}}{\partial \bar{x}^{\alpha}} \frac{\partial A_{\gamma}}{\partial x^{\delta}} \, - \, \frac{\partial x^{\delta}}{\partial \bar{x}^{\alpha}} \frac{\partial x^{\gamma}}{\partial \bar{x}^{\beta}} \frac{\partial A_{\delta}}{\partial x^{\gamma}} \\ & = \, \frac{\partial x^{\delta}}{\partial \bar{x}^{\alpha}} \frac{\partial x^{\gamma}}{\partial \bar{x}^{\beta}} \, \left( \frac{\partial A_{\gamma}}{\partial x^{\delta}} \, - \, \frac{\partial A_{\delta}}{\partial x^{\gamma}} \right) \\ & = \, \frac{\partial x^{\delta}}{\partial \bar{x}^{\alpha}} \frac{\partial x^{\gamma}}{\partial \bar{x}^{\beta}} \, F_{\delta \gamma} \ . \end{align}

This definition implies that the electromagnetic field satisfies

which incorporates Faraday's law of induction and Gauss's law for magnetism. This is seen by

= \, \partial_\lambda \partial_\mu A_\nu - \partial_\lambda \partial_\nu A_\mu + \partial_\mu \partial_\nu A_\lambda - \partial_\mu \partial_\lambda A_\nu + \partial_\nu \partial_\lambda A_\mu - \partial_\nu \partial_\mu A_\lambda \, = 0 \,.

Although there appear to be 64 equations in Faraday-Gauss, it actually reduces to just four independent equations. Using the antisymmetry of the electromagnetic field one can either reduce to an identity (0 = 0) or render redundant all the equations except for those with λ,μ,ν = either 1,2,3 or 2,3,0 or 3,0,1 or 0,1,2.

The Faraday-Gauss equation is sometimes written

where the semicolon indicates a covariant derivative, comma indicate a partial derivative, and square brackets indicate anti-symmetrization (see Ricci calculus for the notation). The covariant derivative of the electromagnetic field is

where Γαβ γ is the Christoffel symbol which is symmetric in its lower indices.

Read more about this topic:  Maxwell's Equations In Curved Spacetime

Famous quotes containing the word field:

    “What though the field be lost?
    All is not lost; the unconquerable Will,
    And study of revenge, immortal hate,
    And courage never to submit or yield:
    And what is else not to be overcome?”
    —John Milton (1608–1674)