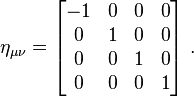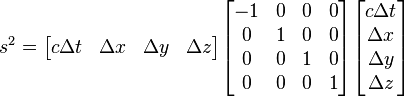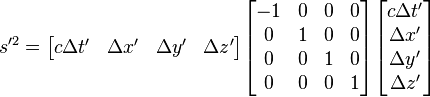Lorentz Transformation - Spacetime Interval

Spacetime Interval

In a given coordinate system xμ, if two events A and B are separated by

the spacetime interval between them is given by

This can be written in another form using the Minkowski metric. In this coordinate system,

Then, we can write

or, using the Einstein summation convention,

Now suppose that we make a coordinate transformation xμ → x′ μ. Then, the interval in this coordinate system is given by

or

It is a result of special relativity that the interval is an invariant. That is, s2 = s′ 2. For this to hold, it can be shown that it is necessary (but not sufficient) for the coordinate transformation to be of the form

Here, Cμ is a constant vector and Λμ_ν a constant matrix, where we require that

Such a transformation is called a Poincaré transformation or an inhomogeneous Lorentz transformation. The Ca represents a spacetime translation. When Ca = 0, the transformation is called an homogeneous Lorentz transformation, or simply a Lorentz transformation.

Taking the determinant of

gives us

The cases are:

• Proper Lorentz transformations have det(Λμ_ν) = +1, and form a subgroup called the special orthogonal group SO(1,3).
• Improper Lorentz transformations are det(Λμ_ν) = −1, which do not form a subgroup, as the product of any two improper Lorentz transformations will be a proper Lorentz transformation.

From the above definition of Λ it can be shown that (Λ0₀)2 ≥ 1, so either Λ0₀ ≥ 1 or Λ0₀ ≤ −1, called orthochronous and non-orthochronous respectively. An important subgroup of the proper Lorentz transformations are the proper orthochronous Lorentz transformations which consist purely of boosts and rotations. Any Lorentz transform can be written as a proper orthochronous, together with one or both of the two discrete transformations; space inversion P and time reversal T, whose non-zero elements are:

The set of Poincaré transformations satisfies the properties of a group and is called the Poincaré group. Under the Erlangen program, Minkowski space can be viewed as the geometry defined by the Poincaré group, which combines Lorentz transformations with translations. In a similar way, the set of all Lorentz transformations forms a group, called the Lorentz group.

A quantity invariant under Lorentz transformations is known as a Lorentz scalar.