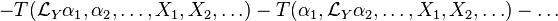Lie Derivative - Lie Derivative of Tensor Fields

Lie Derivative of Tensor Fields

More generally, if we have a differentiable tensor field T of rank and a differentiable vector field Y (i.e. a differentiable section of the tangent bundle TM), then we can define the Lie derivative of T along Y. Let φ:M×R→M be the one-parameter semigroup of local diffeomorphisms of M induced by the vector flow of Y and denote φ_t(p) := φ(p, t). For each sufficiently small t, φ_t is a diffeomorphism from a neighborhood in M to another neighborhood in M, and φ₀ is the identity diffeomorphism. The Lie derivative of T is defined at a point p by

.

where is the pushforward along the diffeomorphism and is the pullback along the diffeomorphism. Intuitively, if you have a tensor field and a vector field Y, then is the infinitesimal change you would see when you flow using the vector field -Y, which is the same thing as the infinitesimal change you would see in if you yourself flowed along the vector field Y.

We now give an algebraic definition. The algebraic definition for the Lie derivative of a tensor field follows from the following four axioms:

Axiom 1. The Lie derivative of a function is the directional derivative of the function. So if f is a real valued function on M, then

Axiom 2. The Lie derivative obeys the Leibniz rule. For any tensor fields S and T, we have

Axiom 3. The Lie derivative obeys the Leibniz rule with respect to contraction

Axiom 4. The Lie derivative commutes with exterior derivative on functions

Taking the Lie derivative of the relation then easily shows that that the Lie derivative of a vector field is the Lie bracket. So if X is a vector field, one has

The Lie derivative of a differential form is the anticommutator of the interior product with the exterior derivative. So if α is a differential form,

This follows easily by checking that the expression commutes with exterior derivative, is a derivation (being an anticommutator of graded derivations) and does the right thing on functions.

Explicitly, let T be a tensor field of type (p,q). Consider T to be a differentiable multilinear map of smooth sections α1, α2, ..., αq of the cotangent bundle T*M and of sections X₁, X₂, ... X_p of the tangent bundle TM, written T(α1, α2, ..., X₁, X₂, ...) into R. Define the Lie derivative of T along Y by the formula

The analytic and algebraic definitions can be proven to be equivalent using the properties of the pushforward and the Leibniz rule for differentiation. Note also that the Lie derivative commutes with the contraction.