Language Model - N-gram Models

N-gram Models

In an n-gram model, the probability of observing the sentence w1,...,wm is approximated as

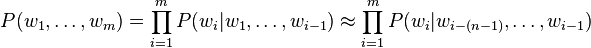
P(w_1,\ldots,w_m) = \prod^m_{i=1} P(w_i|w_1,\ldots,w_{i-1}) \approx \prod^m_{i=1} P(w_i|w_{i-(n-1)},\ldots,w_{i-1})

Here, it is assumed that the probability of observing the ith word wi in the context history of the preceding i-1 words can be approximated by the probability of observing it in the shortened context history of the preceding n-1 words (nth order Markov property).

The conditional probability can be calculated from n-gram frequency counts: 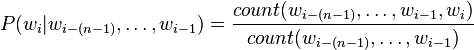P(w_i|w_{i-(n-1)},\ldots,w_{i-1}) = \frac{count(w_{i-(n-1)},\ldots,w_{i-1},w_i)}{count(w_{i-(n-1)},\ldots,w_{i-1})}

The words bigram and trigram language model denote n-gram language models with n=2 and n=3, respectively.

Typically, however, the n-gram probabilities are not derived directly from the frequency counts, because models derived this way have severe problems when confronted with any n-grams that have not explicitly been seen before. Instead, some form of smoothing is necessary, assigning some of the total probability mass to unseen words or N-grams. Various methods are used, from simple "add-one" smoothing (assign a count of 1 to unseen N-grams) to more sophisticated models, such as Good-Turing discounting or back-off models.

Read more about this topic:  Language Model

Famous quotes containing the word models:

    “Friends broaden our horizons. They serve as new models with whom we can identify. They allow us to be ourselves—and accept us that way. They enhance our self-esteem because they think we’re okay, because we matter to them. And because they matter to us—for various reasons, at various levels of intensity—they enrich the quality of our emotional life.”
    —Judith Viorst (20th century)