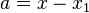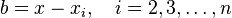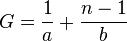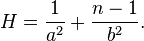Laguerre's Method - Derivation

Derivation

The fundamental theorem of algebra states that every nth degree polynomial p can be written in the form

where x_k are the roots of the polynomial. If we take the natural logarithm of both sides, we find that

Denote the derivative by

and the negated second derivative by

We then make what Acton calls a 'drastic set of assumptions', that the root we are looking for, say, is a certain distance away from our guess, and all the other roots are clustered together some distance away. If we denote these distances by

$a = x - x_1 \,$

and

$b = x - x_i,\quad i = 2, 3,\ldots, n$

then our equation for G may be written

$G = \frac{1}{a} + \frac{n - 1}{b}$

and that for H becomes

$H = \frac{1}{a^2} + \frac{n-1}{b^2}.$

Solving these equations, we find that

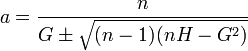$a = \frac{n}{G \plusmn \sqrt{(n-1)(nH - G^2)}}$ ,

where the square root of a complex number is chosen to produce larger absolute value of the denominator, or equivalently, to satisfy:, where denotes real part of a complex number, and is a complex conjugation of ; or

$a = \frac{p(x)}{p'(x)}\cdot \left( \frac1n+\frac{n-1}n\,\sqrt{1-\frac{n}{n-1}\,\frac{p(x)p''(x)}{p'(x)^2}} \right)^{-1}$ ,

where the square root of a complex number is chosen to have a non-negative real part. For small values of p(x) this formula differs from the offset of the third order Halley's method by an error of .

Note that, even if the 'drastic set of assumptions' does not work for some particular polynomial P, P can be transformed into a related polynomial Q for which the assumptions are correct, e.g. by adding a suitable complex number to give distinct roots distinct magnitudes if necessary (which it will be if some roots are complex conjugates), and then repeatedly applying the root squaring transformation used in Graeffe's method enough times to make the smaller roots significantly smaller than the largest root (and so, clustered in comparison); the Graeffe's method approximation can be used to start the new iteration for Laguerre's method. An approximate root for P may then be obtained straightforwardly from that for Q.

Read more about this topic: Laguerre's Method