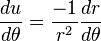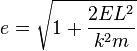Kepler Problem - Solution of The Kepler Problem

Solution of The Kepler Problem

The equation of motion for the radius of a particle of mass moving in a central potential is given by Lagrange's equations

m\frac{d^{2}r}{dt^{2}} - mr \omega^{2} = m\frac{d^{2}r}{dt^{2}} - \frac{L^{2}}{mr^{3}} = -\frac{dV}{dr}


and the angular momentum is conserved. For illustration, the first term on the left-hand side is zero for circular orbits, and the applied inwards force equals the centripetal force requirement, as expected.

If L is not zero the definition of angular momentum allows a change of independent variable from to

\frac{d}{dt} = \frac{L}{mr^{2}} \frac{d}{d\theta}

giving the new equation of motion that is independent of time

\frac{L}{r^{2}} \frac{d}{d\theta} \left( \frac{L}{mr^{2}} \frac{dr}{d\theta} \right)- \frac{L^{2}}{mr^{3}} = -\frac{dV}{dr}

The expansion of the first term is

\frac{L}{r^{2}} \frac{d}{d\theta} \left( \frac{L}{mr^{2}} \frac{dr}{d\theta} \right) = \frac{L^{2}}{mr^{5}} \left( \frac{dr}{d\theta} \right)^2 - \frac{L^{2}}{mr^{4}} \frac{d^{2}r}{d\theta^{2}}


This equation becomes quasilinear on making the change of variables and multiplying both sides by

\frac{du}{d\theta} = \frac{-1}{r^{2}} \frac{dr}{d\theta}
\frac{d^{2}u}{d^{2}\theta^{2}} = \frac{2}{r^{3}} \left( \frac{dr}{d\theta} \right)^{2} - \frac{1}{r^{2}} \frac{d^{2}r}{d\theta^{2}}

After substitution and rearrangement:

\frac{d^{2}u}{d\theta^{2}} + u = -\frac{m}{L^{2}} \frac{d}{du} V(1/u)

For an inverse-square force law such as the gravitational or electrostatic potential, the potential can be written

V(\mathbf{r}) = \frac{k}{r} = ku

The orbit can be derived from the general equation

\frac{d^{2}u}{d\theta^{2}} + u = -\frac{m}{L^{2}} \frac{d}{du} V(1/u) = -\frac{km}{L^{2}}

whose solution is the constant plus a simple sinusoid

u \equiv \frac{1}{r} = -\frac{km}{L^{2}} \left

where (the eccentricity) and (the phase offset) are constants of integration.

This is the general formula for a conic section that has one focus at the origin; corresponds to a circle, corresponds to an ellipse, corresponds to a parabola, and corresponds to a hyperbola. The eccentricity is related to the total energy (cf. the Laplace–Runge–Lenz vector)

e = \sqrt{1 + \frac{2EL^{2}}{k^{2}m}}

Comparing these formulae shows that corresponds to an ellipse (all solutions which are closed orbits are ellipses), corresponds to a parabola, and corresponds to a hyperbola. In particular, for perfectly circular orbits (the central force exactly equals the centripetal force requirement, which determines the required angular velocity for a given circular radius).

For a repulsive force (k > 0) only e > 1 applies.

Read more about this topic:  Kepler Problem

Famous quotes containing the words solution of the, solution of, solution and/or problem:

    “What is history? Its beginning is that of the centuries of systematic work devoted to the solution of the enigma of death, so that death itself may eventually be overcome. That is why people write symphonies, and why they discover mathematical infinity and electromagnetic waves.”
    —Boris Pasternak (1890–1960)

    “Give a scientist a problem and he will probably provide a solution; historians and sociologists, by contrast, can offer only opinions. Ask a dozen chemists the composition of an organic compound such as methane, and within a short time all twelve will have come up with the same solution of CH4. Ask, however, a dozen economists or sociologists to provide policies to reduce unemployment or the level of crime and twelve widely differing opinions are likely to be offered.”
    —Derek Gjertsen, British scientist, author. Science and Philosophy: Past and Present, ch. 3, Penguin (1989)

    “To the questions of the officiously meddling police Falter replied absently and tersely; but, when he finally grew tired of this pestering, he pointed out that, having accidentally solved “the riddle of the universe,” he had yielded to artful exhortation and shared that solution with his inquisitive interlocutor, whereupon the latter had died of astonishment.”
    —Vladimir Nabokov (1899–1977)

    “The problem ... is emblematic of what hasn’t changed during the equal opportunity revolution of the last 20 years. Doors opened; opportunities evolved. Law, institutions, corporations moved forward. But many minds did not.”
    —Anna Quindlen (b. 1952)