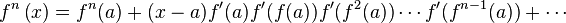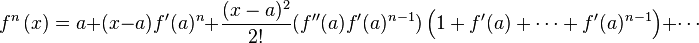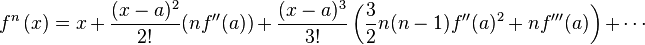Iterated Function - Formulae For Fractional Iteration

Formulae For Fractional Iteration

One method of finding a series formula for fractional iteration, making use of a fixed point, is as follows.

(1) First determine a fixed point for the function such that f(a)=a.

(2) Define for all n belonging to the reals. This in some ways is the most natural extra condition to place upon the fractional iterates.

(3) Expand around the fixed point a as a Taylor series.

f^n(x) = f^n(a) + (x-a)\frac{d}{dx}f^n(x)|_{x=a} + \frac{(x-a)^2}{2!}\frac{d^2}{dx^2}f^n(x)|_{x=a} +\cdots

(4) Expand out:

f^n\left(x\right) = f^n(a) + (x-a) f'(a)f'(f(a))f'(f^2(a))\cdots f'(f^{n-1}(a)) + \cdots

(5) Substitute in for :

f^n\left(x\right) = a + (x-a) f'(a)^{n} + \frac{(x-a)^2}{2!}(f''(a)f'(a)^{n-1})\left(1+f'(a)+\cdots+f'(a)^{n-1} \right)+\cdots

(6) Make use of geometric progression to simplify terms.

f^n\left(x\right) = a + (x-a) f'(a)^{n} + \frac{(x-a)^2}{2!}(f''(a)f'(a)^{n-1})\frac{f'(a)^n-1}{f'(a)-1}+\cdots

(6b) There is a special case when f'(a)=1:

f^n\left(x\right) = x + \frac{(x-a)^2}{2!}(n f''(a))+ \frac{(x-a)^3}{3!}\left(\frac{3}{2}n(n-1) f''(a)^2 + n f'''(a)\right)+\cdots

(7) When n is not an integer we make use of the power formula

This can be carried on indefinitely although the latter terms become increasingly complicated.

Read more about this topic:  Iterated Function

Famous quotes containing the words formulae and/or fractional:

    “I don’t believe in providence and fate, as a technologist I am used to reckoning with the formulae of probability.”
    —Max Frisch (1911–1991)

    “Hummingbird
    stay for a fractional sharp
    sweetness, and’s gone, can’t take
    more than that.”
    —Denise Levertov (b. 1923)