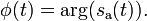The notions of instantaneous phase and instantaneous frequency are important concepts in signal processing that occur in the context of the representation and analysis of time-varying functions.
The instantaneous phase (or "local phase" or simply "phase") of a complex-valued function is the real-valued function
 (See arg function.)
(See arg function.)
And for a real-valued function, it is determined from the function's analytic representation, :
When is constrained to an interval such as or it is called the wrapped phase. Otherwise it is called unwrapped, which is a continuous function of argument assuming is a continuous function of Unless otherwise indicated, the continuous form should be inferred.
Read more about Instantaneous Phase: Examples, Instantaneous Frequency, Complex Representation
Famous quotes containing the word phase:
“The problem of the twentieth century is the problem of the color-line—the relation of the darker to the lighter races of men in Asia and Africa, in America and the islands of the sea. It was a phase of this problem that caused the Civil War.”
—W.E.B. (William Edward Burghardt)