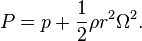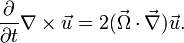Inertial Wave - Mathematical Description

Mathematical Description

Fluid flow is governed by the momentum equation (often called the Navier-Stokes equation) which is essentially a statement of Newton's second law for the fluid. The velocity in a fluid with viscosity under pressure and rotating at rate changes over time according to

\frac{\partial \vec{u}}{\partial t} + (\vec{u} \cdot \vec{\nabla}) \vec{u} = - \frac{1}{\rho} \vec{\nabla}P + \nu \nabla^2 \vec{u} - 2\vec{\Omega} \times \vec{u}.

To be precise, is the velocity of the fluid as observed in the rotating frame of reference. Since a rotating frame of reference is accelerating (i.e. non-inertial frame), two additional (pseudo)forces (as mentioned above) emerges as the result of this coordinate transformation: the centrifugal force and the Coriolis force. In the equation above, the centrifugal force is included as a part of the generalized pressure, that is, is related to the usual pressure, depending on the distance from the rotation axis, by

P = p + \frac{1}{2} \rho r^2 \Omega^2.

The last term on the right side of the momentum equation is the Coriolis term. The first term on the right accounts for pressure, and the second accounts for viscous diffusion.

In the case where the rotation rate is large, the Coriolis force and the centripetal force become large compared to the other terms. Being small in comparison, diffusion and the "convective derivative" (second term on the left) can be left out. Taking a curl of both sides and applying a few vector identities, the result is

\frac{\partial}{\partial t} \nabla \times \vec{u} = 2 ( \vec{\Omega} \cdot \vec{\nabla} ) \vec{u}.

One class of solutions to this equation are waves that satisfy two conditions. First, if is the wave vector,

\vec{u} \cdot \vec{k} = 0,

that is, the waves must be transverse, as mentioned above. Second, solutions are required to have a frequency that satisfies the dispersion relation

\omega = 2 \hat{k} \cdot \vec{\Omega} = 2 \Omega \cos{\theta},

where is the angle between the axis of rotation and the direction of the wave. These particular solutions are known as inertial waves.

The dispersion relation looks much like the Coriolis term in the momentum equation—notice the rotation rate and the factor of two. It immediately implies the range of possible frequencies for inertial waves, as well as the dependence of their frequency on their direction.

Read more about this topic:  Inertial Wave

Famous quotes containing the words mathematical and/or description:

    “An accurate charting of the American woman’s progress through history might look more like a corkscrew tilted slightly to one side, its loops inching closer to the line of freedom with the passage of time—but like a mathematical curve approaching infinity, never touching its goal. . . . Each time, the spiral turns her back just short of the finish line.”
    —Susan Faludi (20th century)

    “The Sage of Toronto ... spent several decades marveling at the numerous freedoms created by a “global village” instantly and effortlessly accessible to all. Villages, unlike towns, have always been ruled by conformism, isolation, petty surveillance, boredom and repetitive malicious gossip about the same families. Which is a precise enough description of the global spectacle’s present vulgarity.”
    —Guy Debord (b. 1931)