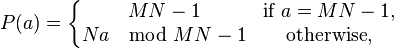In-place Matrix Transposition - Properties of The Permutation

Properties of The Permutation

In the following, we assume that the N×M matrix is stored in row-major order with zero-based indices. This means that the (n,m) element, for n = 0,…,N−1 and m = 0,…,M−1, is stored at an address a = Mn + m (plus some offset in memory, which we ignore). In the transposed M×N matrix, the corresponding (m,n) element is stored at the address a' = Nm + n, again in row-major order. We define the transposition permutation to be the function a' = P(a) such that:

for all

This defines a permutation on the numbers .

It turns out that one can define simple formulas for P and its inverse (Cate & Twigg, 1977). First:

where "mod" is the modulo operation. Proof: if 0 ≤ a = Mn + m < MN − 1, then Na mod (MN−1) = MN n + Nm mod (MN − 1) = n + Nm. Note that the first (a = 0) and last (a = MN−1) elements are always left invariant under transposition. Second, the inverse permutation is given by:

(This is just a consequence of the fact that the inverse of an N×M transpose is an M×N transpose, although it is also easy to show explicitly that P−1 composed with P gives the identity.)

As proved by Cate & Twigg (1977), the number of fixed points (cycles of length 1) of the permutation is precisely 1 + gcd(N−1,M−1), where gcd is the greatest common divisor. For example, with N = M the number of fixed points is simply N (the diagonal of the matrix). If N − 1 and M − 1 are coprime, on the other hand, the only two fixed points are the upper-left and lower-right corners of the matrix.

The number of cycles of any length k>1 is given by (Cate & Twigg, 1977):

where μ is the Möbius function and the sum is over the divisors d of k.

Furthermore, the cycle containing a=1 (i.e. the second element of the first row of the matrix) is always a cycle of maximum length L, and the lengths k of all other cycles must be divisors of L (Cate & Twigg, 1977).

For a given cycle C, every element has the same greatest common divisor . Proof (Brenner, 1973): Let s be the smallest element of the cycle, and . From the definition of the permutation P above, every other element x of the cycle is obtained by repeatedly multiplying s by N modulo MN−1, and therefore every other element is divisible by d. But, since N and MN − 1 are coprime, x cannot be divisible by any factor of MN − 1 larger than d, and hence . This theorem is useful in searching for cycles of the permutation, since an efficient search can look only at multiples of divisors of MN−1 (Brenner, 1973).

Laflin & Brebner (1970) pointed out that the cycles often come in pairs, which is exploited by several algorithms that permute pairs of cycles at a time. In particular, let s be the smallest element of some cycle C of length k. It follows that MN−1−s is also an element of a cycle of length k (possibly the same cycle). Proof: by the definition of P above, the length k of the cycle containing s is the smallest k > 0 such that . Clearly, this is the same as the smallest k>0 such that, since we are just multiplying both sides by −1, and .