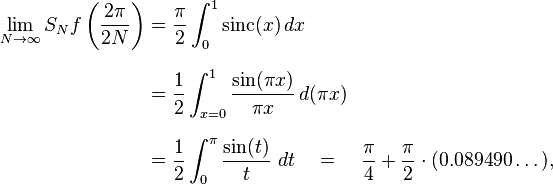Gibbs Phenomenon - The Square Wave Example

The Square Wave Example

We now illustrate the above Gibbs phenomenon in the case of the square wave described earlier. In this case the period L is, the discontinuity is at zero, and the jump a is equal to . For simplicity let us just deal with the case when N is even (the case of odd N is very similar). Then we have

Substituting, we obtain

as claimed above. Next, we compute

S_N f\left(\frac{2\pi}{2N}\right) = \sin\left(\frac{\pi}{N}\right) + \frac{1}{3} \sin\left(\frac{3\pi}{N}\right) + \cdots + \frac{1}{N-1} \sin\left( \frac{(N-1)\pi}{N} \right).

If we introduce the normalized sinc function, we can rewrite this as

S_N f\left(\frac{2\pi}{2N}\right) = \frac{\pi}{2} \left[ \frac{2}{N} \operatorname{sinc}\left(\frac{1}{N}\right) + \frac{2}{N} \operatorname{sinc}\left(\frac{3}{N}\right) + \cdots + \frac{2}{N} \operatorname{sinc}\left( \frac{(N-1)}{N} \right) \right].

But the expression in square brackets is a numerical integration approximation to the integral (more precisely, it is a midpoint rule approximation with spacing ). Since the sinc function is continuous, this approximation converges to the actual integral as . Thus we have

\begin{align} \lim_{N \to \infty} S_N f\left(\frac{2\pi}{2N}\right) & = \frac{\pi}{2} \int_0^1 \operatorname{sinc}(x)\, dx \\ & = \frac{1}{2} \int_{x=0}^1 \frac{\sin(\pi x)}{\pi x}\, d(\pi x) \\ & = \frac{1}{2} \int_0^\pi \frac{\sin(t)}{t}\ dt \quad = \quad \frac{\pi}{4} + \frac{\pi}{2} \cdot (0.089490\dots), \end{align}

which was what was claimed in the previous section. A similar computation shows

\lim_{N \to \infty} S_N f\left(-\frac{2\pi}{2N}\right) = -\frac{\pi}{2} \int_0^1 \operatorname{sinc}(x)\ dx = -\frac{\pi}{4} - \frac{\pi}{2} \cdot (0.089490\dots).

Read more about this topic:  Gibbs Phenomenon

Famous quotes containing the words square and/or wave:

    “I would say it was the coffin of a midget
    Or a square baby
    Were there not such a din in it.”
    —Sylvia Plath (1932–1963)

    “Down the blue night the unending columns press
    In noiseless tumult, break and wave and flow,”
    —Rupert Brooke (1887–1915)