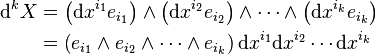Geometric Calculus - Integration

Integration

Let be a set of basis vectors that span an n-dimensional vector space. From geometric algebra, we interpret the pseudoscalar to be the signed volume of the n-parallelotope subtended by these basis vectors. If the basis vectors are orthonormal, then this is the unit pseudoscalar.

More generally, we may restrict ourselves to a subset of k of the basis vectors, where, to treat the length, area, or other general k-volume of a subspace in the overall n-dimensional vector space. We denote these selected basis vectors by . A general k-volume of the k-parallelotope subtended by these basis vectors is the grade k multivector .

Even more generally, we may consider a new set of vectors proportional to the k basis vectors, where each of the is a component that scales one of the basis vectors. We are free to choose components as infinitesimally small as we wish as long as they remain nonzero. Since the outer product of these terms can be interpreted as a k-volume, a natural way to define a measure is

\begin{align}\mathrm{d}^kX &= \left(\mathrm{d}x^{i_1} e_{i_1}\right) \wedge \left(\mathrm{d}x^{i_2}e_{i_2}\right) \wedge\cdots\wedge \left(\mathrm{d}x^{i_k}e_{i_k}\right) \\ &= \left( e_{i_1}\wedge e_{i_2}\wedge\cdots\wedge e_{i_k} \right) \mathrm{d}x^{i_1} \mathrm{d}x^{i_2} \cdots \mathrm{d}x^{i_k}\end{align}

The measure is therefore always proportional to the unit pseudoscalar of a k-dimensional subspace of the vector space. Compare the Riemannian volume form in the theory of differential forms. The integral is taken with respect to this measure:

More formally, consider some directed volume V of the subspace. We may divide this volume into a sum of simplices. Let be the coordinates of the vertices. At each vertex we assign a measure as the average measure of the simplices sharing the vertex. Then the integral of F(x) with respect to U(x) over this volume is obtained in the limit of finer partitioning of the volume into smaller simplices:

Read more about this topic:  Geometric Calculus

Famous quotes containing the word integration:

    “The more specific idea of evolution now reached is—a change from an indefinite, incoherent homogeneity to a definite, coherent heterogeneity, accompanying the dissipation of motion and integration of matter.”
    —Herbert Spencer (1820–1903)

    “Look back, to slavery, to suffrage, to integration and one thing is clear. Fashions in bigotry come and go. The right thing lasts.”
    —Anna Quindlen (b. 1952)

    “The only phenomenon with which writing has always been concomitant is the creation of cities and empires, that is the integration of large numbers of individuals into a political system, and their grading into castes or classes.... It seems to have favored the exploitation of human beings rather than their enlightenment.”
    —Claude Lévi-Strauss (b. 1908)