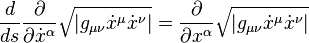Geodesic (general Relativity) - Geodesics As Extremal Curves

Geodesics As Extremal Curves

A geodesic between two events could also be described as the curve joining those two events which has the maximum possible length in time — for a timelike curve — or the minimum possible length in space — for a spacelike curve. The four-length of a curve in spacetime is

Then, the Euler-Lagrange equation,

{d \over ds} {\partial \over \partial \dot x^\alpha} \sqrt{\left| g_{\mu \nu} \dot x^\mu \dot x^\nu \right|} = {\partial \over \partial x^\alpha} \sqrt{\left| g_{\mu \nu} \dot x^\mu \dot x^\nu \right|}

becomes, after some calculation,

Proof

The goal being to extremize the value of

where

such goal can be accomplished by calculating the Euler-Lagrange equation for f, which is

.

Substituting the expression of f into the Euler-Lagrange equation (which extremizes the value of the integral l), gives

Now calculate the derivatives:

This is just one step away from the geodesic equation.

If the parameter s is chosen to be affine, then the right side the above equation vanishes (because is constant). Finally, we have the geodesic equation

Read more about this topic:  Geodesic (general Relativity)

Famous quotes containing the word curves:

    “One way to do it might be by making the scenery penetrate the automobile. A polished black sedan was a good subject, especially if parked at the intersection of a tree-bordered street and one of those heavyish spring skies whose bloated gray clouds and amoeba-shaped blotches of blue seem more physical than the reticent elms and effusive pavement. Now break the body of the car into separate curves and panels; then put it together in terms of reflections.”
    —Vladimir Nabokov (1899–1977)