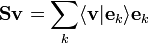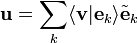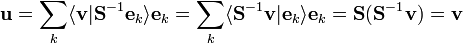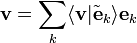Frame of A Vector Space - The Dual Frame

The Dual Frame

The frame condition is both sufficient and necessary for allowing the construction of a dual or conjugate frame, relative the original frame, . The duality of this frame implies that

$\sum_{k} \langle \mathbf{v} | \mathbf{\tilde{e}}_{k} \rangle \mathbf{e}_{k} = \sum_{k} \langle \mathbf{v} | \mathbf{e}_{k} \rangle \mathbf{\tilde{e}}_{k} = \mathbf{v}$

is satisfied for all . In order to construct the dual frame, we first need the linear mapping: defined as

$\mathbf{S} \mathbf{v} = \sum_{k} \langle \mathbf{v} | \mathbf{e}_{k} \rangle \mathbf{e}_{k}$

From this definition of and linearity in the first argument of the inner product, it now follows that

$\langle \mathbf{S} \mathbf{v} | \mathbf{v} \rangle = \sum_{k} |\langle \mathbf{v} | \mathbf{e}_{k} \rangle|^{2}$

which can be inserted into the frame condition to get

$A \| \mathbf{v} \|^{2} \leq \langle \mathbf{S} \mathbf{v} | \mathbf{v} \rangle \leq B \| \mathbf{v} \|^{2} \text{ for all }\mathbf{v} \in V$

The properties of can be summarised as follows:

is self-adjoint, positive definite, and has positive upper and lower bounds. This leads to
the inverse of exists and it, too, is self-adjoint, positive definite, and has positive upper and lower bounds.

The dual frame is defined by mapping each element of the frame with :

$\tilde{\mathbf{e}}_{k} = \mathbf{S}^{-1} \mathbf{e}_{k}$

To see that this make sense, let be arbitrary and set

$\mathbf{u} = \sum_{k} \langle \mathbf{v} | \mathbf{e}_{k} \rangle \tilde{\mathbf{e}}_{k}$

It is then the case that

$\mathbf{u} = \sum_{k} \langle \mathbf{v} | \mathbf{e}_{k} \rangle ( \mathbf{S}^{-1} \mathbf{e}_{k} ) = \mathbf{S}^{-1} \left ( \sum_{k} \langle \mathbf{v} | \mathbf{e}_{k} \rangle \mathbf{e}_{k} \right ) = \mathbf{S}^{-1} \mathbf{S} \mathbf{v} = \mathbf{v}$

which proves that

$\mathbf{v} = \sum_{k} \langle \mathbf{v} | \mathbf{e}_{k} \rangle \tilde{\mathbf{e}}_{k}$

Alternatively, we can set

$\mathbf{u} = \sum_{k} \langle \mathbf{v} | \tilde{\mathbf{e}}_{k} \rangle \mathbf{e}_{k}$

By inserting the above definition of and applying known properties of and its inverse, we get

$\mathbf{u} = \sum_{k} \langle \mathbf{v} | \mathbf{S}^{-1} \mathbf{e}_{k} \rangle \mathbf{e}_{k} = \sum_{k} \langle \mathbf{S}^{-1} \mathbf{v} | \mathbf{e}_{k} \rangle \mathbf{e}_{k} = \mathbf{S} (\mathbf{S}^{-1} \mathbf{v}) = \mathbf{v}$

which shows that

$\mathbf{v} = \sum_{k} \langle \mathbf{v} | \tilde{\mathbf{e}}_{k} \rangle \mathbf{e}_{k}$

This derivation of the dual frame is a summary of section 3 in the article by Duffin and Schaeffer. They use the term conjugate frame for what here is called dual frame.

Read more about this topic: Frame Of A Vector Space

Famous quotes containing the words dual and/or frame:

“Thee for my recitative,
Thee in the driving storm even as now, the snow, the winter-day
declining,
Thee in thy panoply, thy measur’d dual throbbing and thy beat
convulsive,
Thy black cylindric body, golden brass and silvery steel,”
—Walt Whitman (1819–1892)

“I frame no hypotheses; for whatever is not deduced from the phenomena is to be called a hypothesis; and hypotheses, whether metaphysical or physical, whether of occult qualities or mechanical, have no place in experimental philosophy.”
—Isaac Newton (1642–1727)