Forces Acting On A Half-plane
For the special case where, the wedge is converted into a half-plane with a normal force and a tangential force. In that case
Therefore the stresses are
and the displacements are (using Michell's solution)
The dependence of the displacements implies that the displacement grows the further one moves from the point of application of the force (and is unbounded at infinity). This feature of the Flamant solution is confusing and appears unphysical. For a discussion of the issue see http://imechanica.org/node/319.
Read more about this topic: Flamant Solution
Famous quotes containing the words forces and/or acting:
“There exists, at the bottom of all abasement and misfortune, a last extreme which rebels and joins battle with the forces of law and respectability in a desperate struggle, waged partly by cunning and partly by violence, at once sick and ferocious, in which it attacks the prevailing social order with the pin-pricks of vice and the hammer-blows of crime.”
—Victor Hugo (1802–1885)
“Its idea of “production value” is spending a million dollars dressing up a story that any good writer would throw away. Its vision of the rewarding movie is a vehicle for some glamour-puss with two expressions and eighteen changes of costume, or for some male idol of the muddled millions with a permanent hangover, six worn-out acting tricks, the build of a lifeguard, and the mentality of a chicken-strangler.”
—Raymond Chandler (1888–1959)

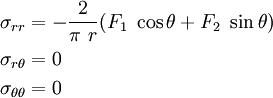
![\begin{align} u_r & = -\cfrac{1}{4\pi\mu}\left[F_1\{(\kappa-1)\theta\sin\theta - \cos\theta + (\kappa+1)\ln r\cos\theta\} + \right. \\ & \qquad \qquad \left. F_2\{(\kappa-1)\theta\cos\theta + \sin\theta - (\kappa+1)\ln r\sin\theta\}\right]\\ u_\theta & = -\cfrac{1}{4\pi\mu}\left[F_1\{(\kappa-1)\theta\cos\theta - \sin\theta - (\kappa+1)\ln r\sin\theta\} - \right. \\ & \qquad \qquad \left. F_2\{(\kappa-1)\theta\sin\theta + \cos\theta + (\kappa+1)\ln r\cos\theta\}\right] \end{align}](http://upload.wikimedia.org/math/4/9/6/496b6f7767598c7f1ed4d634ef2210bb.png)